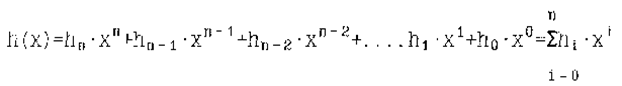ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ПРИНЦИП ПОСТРОЕНИЯ ЛИНЕЙНОГО РЕКУРРЕНТНОГО РЕГИСТРА (ЛРР)
Лекция по учебной дисциплине “Компьютерная безопасность”
Тема № 2.3: Реализация шифров
Лекция № 2: Методы получения случайных и псевдослучайных чисел
Лекция разработана полковником Борисенко Н.П.
Обсуждено на заседании кафедры №33 “ ”______________2000 г. Протокол №____________
Орел 2000 Учебные и воспитательные цели: 1. Изучить вопросы лекции. 2. Активизировать слушателей на изучение вопросов обеспечения безопасности вычислительных систем криптографическими методами. 3. Воспитывать чувство ответственности за организацию и обеспечение информационной безопасности.
Место: Лекционный зал Учебно-материальное обеспечение: _____________________________ ___________________________________________________________
Распределение времени лекции Вступительная часть 5 мин. Учебные вопросы лекции: 1. Генерация случайных и псевдослучайных последовательностей. 2. Способы проверки на случайность. Заключение 5 мин.
Содержание лекции Вступительная часть: Широкое применение для передачи, хранения и приема информации в настоящее время находят цифровые методы обработки сигналов. Реализация указанных методов обработки сигналов осуществляется с помощью различных технических устройств. Рассматриваемые на данной лекции устройства относятся к разряду универсальных или многофункциональных. На базе линейных рекуррентных регистров можно реализовать множество функциональных зависимостей в той или иной степени используемых при цифровой обработки сигналов. Роль линейных рекуррентных регистров особо возрастает при изучении построения узлов специальной техники, поскольку из-за уникальных свойств линейных рекуррентных регистров некоторые узлы специальной техники либо вообще не могут быть реализованы,либо реализация их может быть сопряжена с трудностями технического или экономического характера. В данной лекции последовательно будут рассмотрены принципы построения линейных рекуррентных регистров, математический аппарат положенный в основу анализа и синтеза линейных рекуррентных регистров, отдельные наиболее важные свойства и использование линейных рекуррентных регистров в функциональных узлах специальной техники. Генерация случайных и псевдослучайных последовательностей 1.1.
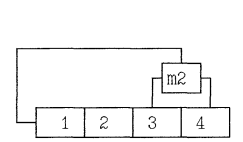
ПРИНЦИП ПОСТРОЕНИЯ ЛИНЕЙНОГО РЕКУРРЕНТНОГО РЕГИСТРА (ЛРР) Линейным рекуррентным регистром называется регистр сдвига с линейной обратной связью (другие обозначения - рекуррентная линия задержки (РЛЗ), одноканальная линия задержки с обратной связью (ОЛЗ), саморазвертка). Переключательная функция Y=F(x1, x2, x3) является линейной, если она может быть описана только с помощью функций неравнозначности (равнозначности). Например Y=x1Åx2Åx3 является линейной, а Y=x1´x2Åx3 - нелинейной. В общем виде ЛРР может быть представлен в виде следующей схемы показанной на рис.1.
Рис.1 где: hi '0,1;
- элемент памяти регистра сдвига Число элементов памяти ЛРР определяет его длину n. Первоначально в ячейки памяти вводится двоичная последовательность, определяющая начальное заполнение А0,А1,......Аn-1. После этого замыкается обратная связь. При поступлении тактовых импульсов содержимое ячеек памяти сдвигается вправо, а в первую ячейку записывается результат сложения по модулю два содержимого ячеек, имеющих отводы. Одновременно с этим с крайней правой ячейки считывается первый элемент входной последовательности. При поступлении следующих тактовых импульсов работа ЛРР происходит аналогичным образом. ЛРР формирует неограниченную двоичную последовательность, которая может быть описана следующими соотношениями
Анализ соотношений показывает, что символы выходной последовательности Вi начиная с n-ого такта полностью определяются своими предыдущими значениями. Поэтому соотношение (1) называется рекуррентным. На рис.2 приведены схемы ЛРР и таблицы изменения состояния их ячеек. Выходная последовательность ЛРР может сниматься с любого разряда регистра. Заметим, что в последовательности состояний ЛРР отсутствует комбинация 0000.... Такая комбинация является запрещенной, так как при записи ее в регистр последний будет генерировать одни 000...
 Рис.2 С целью удобства анализа и синтеза ЛРР используют описание последних с помощью многочленов. Каждому ЛРР длины n можно сопоставить полином обратных связей вида
Причем, всегда hn=1 и h0=1. Так, для приведенного выше примера h(x)=x4+x+1 h(x)=x3+x+1 Свойства характеристического многочлена во многом определяют свойства выходных последовательностей ЛРР. Они изучаются в алгебре, теории чисел, теории конечных полей Галуа. Полином h(x) имеет двойственный многочлен h*(x). Взаимосвязь указанных полиномов выражается следующим соотношением h*(x)=xn h(1/n) Например, для h(x)=x4+x+1 получим h*(x)=x4 (1/x4+1/x+1)=x4+x3+1. Дляh(x)=x3+x+1 двойственный полином h*(x)=x3+x2+1 Полиномы h(x) и h*(x) обладают идентичными свойствами. Однако необходимо помнить, что у двойственного полинома нумерация разрядов ведется слева направо. Например, полиному h*(x)=x4+x3+1 соответствует схема приведенная на рис.3
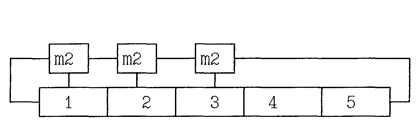
Рис.3 А полиному h*(x)=x5+x3+x2+x+1 соответствует схема приведенная на рис.4.
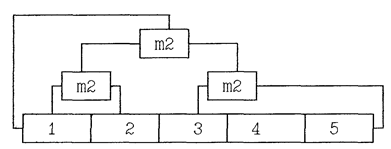
Рис.4 На основании свойства коммутативности функции неравнозначности следует, что соединение схем сложения по модулю два в цепи обратной связи ЛРР может быть любым. Поэтому, схема изображенная на рис. 5 будет эквивалентна вышеприведенной схеме, то есть обе схемы будут формировать одинаковые последовательности.
Рис.5 При построении схем ЛРР по характеристическому полиному h(x) иногда пользуются тем же правилом, что и для h*(x). Некорректность данного приема проявляется лишь тогда, когда важна конфигурация выходной последовательности, например при помехоустойчивом кодировании. Поэтому, когда задан полином h(x)=x4Åx3Åx2Å1, описывающий кодер помехоустойчивого циклического кода (7.4), схема на рис.6 не будет корректной.
Рис.6 Правильный вид схемы показан на рис.7.
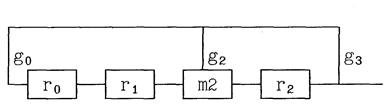
Рис.7 ЛРР может быть построен, если в цепи обратной связи вместо схем неравнозначности включить схемы равнозначности. Легко убедиться , что в этом случае запрещенной комбинацией будет комбинация состоящая из одних единиц. Еще одна разновидность ЛРР получается, если сумматоры по модулю два включить между ячейками памяти (рис.8).
Рис.8 В этом случае нумерация отводов и ячеек памяти производится слева направо и характеристический полином имеет вид g(x)=g3x3+g2x2+g0x0=x3+x2+1 При рассмотрении свойств ЛРР нам потребуются два основных свойства полиномов обратных связей. Определим эти свойства. Полином h(x) называется неприводимым, если его нельзя представить в виде произведения двух или более полиномов ненулевой степени с коэффициентами 0 или 1. Перемножение или сложение коэффициентов полиномов должно осуществляться по модулю два. Например, полином h(x)=x2+1 приводим, так как (x+1) (x+1)=x2+x+x+1=x2+1 А полином h(x)=x3+x+1 является неприводимым. В натуральном ряду чисел имеются их аналоги- простые числа 3,5,7,11,13. |



 ГСЧ на шумовом диоде
ГСЧ на шумовом диоде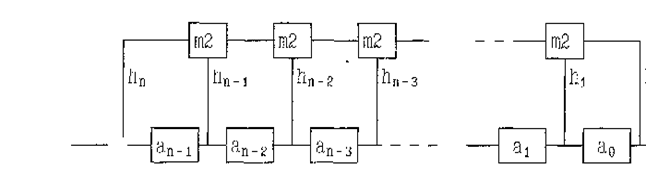

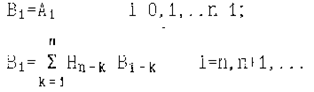 (1)
(1)