 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Расчет температурных напряжений в статически неопределимой стержневой системе
Задача 8
Принять Ем = 1×105 МПа, Ес = 2×105 МПа, aм = 1,65× 10-5, aс = 1,25× 10-5. Решение При нагревании расширению стержня препятствуют недеформируемые стенки, поэтому на торцевых сечениях возникают реакции RB и Rc. При одном возможном уравнении статического равновесия SZ = 0 две неизвестные реакции. Стержень статически неопределим со степенью статической неопределимости m = 1. 1. Статическая сторона задачи Уравнение статического равновесия (рис. 3.6.2)
2. Деформационная сторона задачи Поскольку стержень защемлен, его общее удлинение DL = 0. Общая абсолютная деформация стержня является суммой абсолютных деформаций его ступеней: DL = DlBD + DlDC, абсолютная деформация каждой ступени состоит из температурной деформации и деформации от силы, возникающей от защемления стержня. DlBD = DlBD(t) + DlBD(N), DlDС = DlDС(t) + DlDС(N), тогда уравнение совместности перемещений принимает вид: DlBD(t) + DlBD(N) +DlDС(t) + DlDС(N) = 0. 3. Физическая сторона задачи Температурные деформации: DlBD(t) = aм× lBD× Dt, DlDС(t) = aс× lDС× Dt. Силовая часть деформации по закону Гука
Подставляя в уравнение совместности перемещений, учитывая длины участков и величины Ес == 2Ем (из условия задачи),
после преобразований:
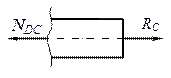
Продольные силы NBD и NDС определим методом сечений (рис. 3.6.3):
После подстановки в уравнение
4. Синтез Система разрешающих уравнений:
подставим RC = RB в первое уравнение:
Тогда напряжения, возникающие на участках стержня:
Таким образом, наибольшие сжимающие напряжения возникают в сечениях стального стержня sDC = 110,67 МПа.
Задача 9
температуры конструкции до t2 = -40°. Принять Ем = 1×105 МПа, Ес = 2×105 МПа, aм = 1,65×10-5, aс = 1,25×10-5. Решение При понижении температуры на Dt = 60° стержни получают температурные абсолютные деформации сжатия Dl(t) = at×l×Dt, где at – коэффициент температурного расширения, l – длина стержня, Dt – изменение температуры. Стержни изготовлены из разных материалов, разной длины, поэтому температурные деформации различны и появляются силовые деформации. 1. Статическая сторона задачи
фициент линейного расширения меди больше, чем у стали, и все стержни соединены в узле С. Запишем уравнения статического равновесия:
В одном уравнении две неизвестные силы. Для получения еще одного уравнения рассмотрим деформационную сторону задачи. 2. Деформационная сторона задачи
тогда
подставим в уравнение
Полученное уравнение является уравнением совместности перемещений. 2. Физическая сторона задачи Температурные деформации
По закону Гука Подставим в уравнение совместности перемещений
После преобразований и учитывая соотношение Ес = 2Ем,
После преобразований
3. Синтез Система разрешающих уравнений
Подставим исходные данные
откуда 9,535N2 = 81А, N2 = 8,495А (МПа×А), тогда N1 = 10,45А (МПа×А). Напряжения в стержнях: в стальном стержне в медном стержне Напряжение в медном стержне со знаком минус, поскольку продольная сила n2 сжимающая.
|



 Рис. 3.6.1
Рис. 3.6.1 Рис. 3.6.2
Рис. 3.6.2 ;
;  .
. ,
,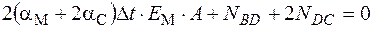 .
.
 .
.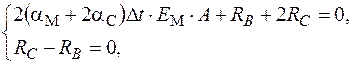
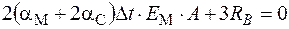 , откуда
, откуда .
. МПа,
МПа, МПа.
МПа. Рис. 3.6.4
Рис. 3.6.4 Рис. 3.6.5
Рис. 3.6.5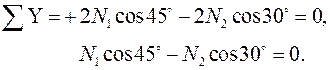
 Рис. 3.6.6
Рис. 3.6.6 , из DСС1С3 отрезок
, из DСС1С3 отрезок 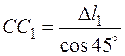 ,
, , перемещение Dl2 является суммой температурной и силовой части деформации
, перемещение Dl2 является суммой температурной и силовой части деформации ,
,  ,
, .
.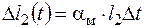 ,
,  .
. ,
,  .
.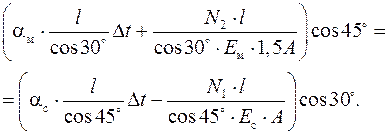
 ,
, .
. или
или .
.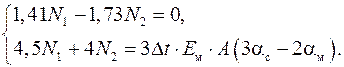
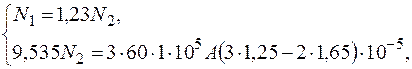
 МПа,
МПа, МПа.
МПа.