 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Персональная электронная вычислительная машина
1) доступная стоимость (из-за большого производства) 2) Достаточный набор для организации человеко-машинного взаимодействия. 3) Наличие операционной системы - операционной среды, обеспечивающей диалоговый (интерактивный) характер общения с пользователем. 4) Наличие средств программирования. 5) Программное обеспечение универсально, т.е. ориентированно на массового пользователя. Микропроцессор - это программно управляемое цифровое устройство в виде одной или нескольких интегральных микросхем (микропроцессорный комплект, chipset). Отличительное свойство - экономичность его изготовления как серийного устройства и универсальность его потребления. Микроконтроллер -интегральная микросхема, содержащая полнофункциональный набор внутренних блоков. Иначе процессоры называют однокристальными микро ЭВМ. Контролирует устройства Позиционные системы счисления могут быть представлены в виде: 1) одноичные (1111111) 2) Двоичные системы счисления - являются основной при построении цифр ЭВМ -проще построение элемента, находящегося в одном из двух состояний: 0 и 1 технологически очень просто. Системы счисления (позиционные - значение числа зависит от позиции цифр; [епозиционные - значение числа зависит от конфигурации).
3)Восьмеричная, шестнадцатеричная - используют только программисты для общения с компьютером. Законы: 1) Закон двойного отрицания: A = A 2) Переместительный (з-н коммутативности): A v B = B v A (сложение) A & B = B & A (умножение) 3) Сочетательный: (A v B) v C = A v (B v C) (A & B)&C = A&( B & C) 4) Распределительный: (A v B)& C = (A & C) v (A & B) (A & B) v C = (A v C)&(B v C) 5) Закон общей инверсии (де Моргана): A v B = A & B A & B = A v B 6) Закон идемпотентности: A v A = A A & A = A 7) Закон исключения констант: A v 1 = 1 A v 0 = A A&1=A A&0=0 8) Закон противоречия: A & A = 0 9) Закон исключения третьего: A & A = 1 10) Закон поглощения: A v (A & B) = A A & (A v B) = A 11) Закон исключения (склеивания): (A & B) v (A & B) = B (A v B)&( A v B) = B 12) Закон контрапозиции (правило перевертывания): (A <=> B) = (B <=> A) 13) Закон тождества: A = A 14) Замена импликации: (A => B = A v B) 15) Замена эквивалентности: A <=>B = (AvB)&(AvB) A <=> B = (A & B) v (A & B) A <=> B = (A => B)& (B => A) Перевод из одной системы счисления в другую. 1) Табличный способ. применим, если происходит преобразование 2n -—2k, либо для небольших значений.
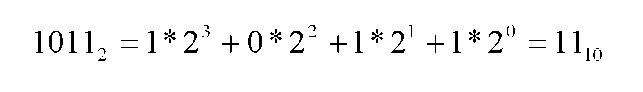 2) Использующий вес разрядов.
3) Метод преобразования чисел из 10-чной системы счисления в систему с Метод деления столбиком.
Перевод дробных чисел. При переводе других чисел необходимо последовательно умножить число в системе А на основание системы В, отделяя после каждого умножения целую часть произведения. Умножение производиться до тех пор, пока дробная часть произведения не станет равной нулю, или не будет получена требуемая точность.
Смешанные числа преобразуются: целая часть своим способом, дробную своим. Пример:
|
При вычислении суммы степенного ряда все операции производятся в той системе счисления, в которой производятся преобразования.
При переводе чисел из системы счисления с основанием А в систему счисления с основанием В необходимо рассматривать 3 случая:
