 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Общие понятия о сверточном кодировании 12
СВЁРТОЧНЫЕ КОДЫ и описание работы сверточного кодера. В течение последнего десятилетия наиболее популярным видом кодирования было свёрточное кодирование, поскольку во многих приложениях свёрточные коды лучше блочных при той же конструктивной сложности кодера и декодера. В разработку сверточных кодов большой вклад внесли американские ученые. Сверточные коды были впервые введены Т.П.Элайсом в 1955году. В отличие от рассмотренных ранее блочных кодов, сверточные коды являются непрерывными. Их кодирование и декодирование осуществляются непрерывно, то есть без деления информационных символов на блоки. Название метода кодирования означает, что последовательность символов на выходе кодера можно рассматривать как свертку импульсной характеристики кодера с входной последовательностью информационных символов. В 1957 году Дж.Возенкрафтом был разработан метод последовательного декодирования для этих кодов, который впоследствии был усовершенствован А.М.Фано Основным рабочим инструментом при разработке кодирующих и декодирующих устройств в то время для сверточных кодов было так называемое кодовое дерево. В 1967 году Д.Форни вместо кодового дерева ввел эквивалентную, но более экономичную (с точки зрения объема вычислений) структуру, получившую название - решетчатая структура. И в том же 1967 году известный американский ученый А.Д. Витерби предложил новый метод декодирования сверточных кодов в виде простой итеративной процедуры, названный его именем – алгоритм декодирования Витерби. В этом методе декодирования вместо кодового дерева используется решетчатая структура. Было установлено, что алгоритм Витерби является методом динамического программирования (которое уже было известно в то время), примененным к сверточным кодам. Сверточное кодирование, применяемое вместе с декодированием Витерби, в настоящее время стало одним из наиболее широко используемых на практике методов исправления ошибок.
При каждом поступлении информационного символа в первую ячейку регистра символы в регистре смещаются на одну позицию вправо. Коммутатор вначале находится в верхнем положении и считывает на выход кодовый символ из верхнего сумматора, а затем переключается в нижнее положение и считывает на выход кодовый символ из нижнего сумматора. После этого на вход регистра поступает следующий информационный символ, происходит новое смещение символов в регистре сдвига и снова коммутатор считывает кодовые символы сначала с верхнего сумматора, а затем с нижнего и так далее. Естественно, что скорость переключения коммутатора должна быть вдвое больше скорости поступления Блочные коды
Отношение Сверточный код описывается тремя целыми числами: - если на вход кодера поступит -если На рис. 2 изображен кодер, для которого параметры
Рис. 2. Сверточный кодер.
На рис. 3 изображен кодер, для которого параметры
Рис. 3. Сверточный кодер.
Третий параметр – целое число Для кодера на рис. 1 величина Существует несколько способов описания связей между разрядами в регистре сдвига и сумматорами по модулю 2: 1. Один из этих способов заключается в определении Единица (1) на
Для кодера на рис. 2 получим векторы связи:
2. Второй способ позволяет представить связи между разрядами регистра и сумматорами в виде набора из Полиномиальные генераторы (или просто полиномы)
Сравнивая (1) с (3), заключаем, что составляющие векторов связи в (1) соответствуют коэффициентам полиномов в (3). С помощью полиномиальных генераторов легко определить кодовые символы на выходе кодера, когда на его вход поступает заданная последовательность информационных символов. Пусть, например, на вход кодера поступает последовательность информационных символов: Этой последовательности соответствует полином
Полином
(значения сумм в круглых скобках определяем по модулю 2).
Полином (здесь сложение не по модулю 2)
Последовательность
Избыточность, которая вводится при сверточном кодировании, позволяет, как и в случае блочных кодов, исправлять определенное количество ошибок, которые появляются на выходе демодулятора из-за действия сигнала помехи. Подробно вопрос декодирования свёрточного кода будет рассмотрен ниже. Отметим, что в определенных случаях при сверточном декодировании возможно возникновение такого явления, как «катастрофическая ошибка». Эта ошибка возникает, когда конечное число ошибок на выходе демодулятора вызывает бесконечное число ошибок на выходе декодера. Исследования показали, что необходимым и достаточным условием для возможного распространения катастрофических ошибок является наличие у полиномиальных генераторов Например, сверточному кодеру, изображенному на рис. 4 соответствуют следующие полиномиальные генераторы:
Рис. 4 Сверточный кодер
Эти генераторы
следовательно, в кодере на рис. 4 может происходить распространение катастрофической ошибки при декодировании. Кодеру рис. 1 , как уже отмечалось, соответствуют полиномиальные генераторы
которые не имеют общего полиномиального множителя степени не менее единицы, поэтому в этом кодере невозможно распространение катастрофической ошибки при декодировании. Рассмотрим работу кодера рис. 1 на двух примерах, при поступлении на его вход двух последовательностей информационных символов. 1. В этом примере на вход кодера подана последовательность информационных символов: 10000 . Реакция кодера на этот входной сигнал является важной характеристикой, которая называется импульсной характеристикойкодера (по аналогии с названием «импульсная характеристика Предположим, что к моменту поступления этой входной последовательности все ячейки регистра сдвига кодера находились в состоянии 0. Тогда, после поступления 1 в первую ячейку регистра на выход кодера через коммутатор будет считана кодовая последовательность 11. Затем, в первую ячейку регистра записывается второй информационный символ входной последовательности, т.е.0, а ее первый символ 1 перейдет во вторую ячейку регистра, в результате чего через коммутатор на выход поступит вторая кодовая последовательность 10. После поступления на вход кодера третьего информационного символа 0 в ячейках регистра будет записана последовательность 001 и на выходе
Таблица 1
коммутатора появится третья кодовая последовательность 11. После поступления на вход кодера четвертого информационного символа 0 в ячейках регистра будет записана последовательность 000 и на выход через коммутатор поступит четвертая кодовая последовательность 00. Рассмотренный пример характеризует таблица 1 и рис. 5.
Рис.5 а) Сигнал на входе кодера, изображенного на рис. 1; б) Напряжение на выходе первой ячейки регистра; в) Сигнал на выходе: импульсная характеристика свёрточного кодера. На рис. 5 введены следующие обозначения:
На рис.5б стрелками показаны моменты переключения коммутатора. Для кодера рис. 1 каждому входному информационному символу соответствуют два кодовых символа на выходе. Поэтому длительность тактового интервала На рис. 5а входной сигнал, соответствующий символу 1, имеет длительность Форму сигнала, соответствующего символу 1, можно изменять, т.е. длительность прямоугольного импульса с амплитудой 1 может быть меньше длительности интервала 2. Рассмотрим работу кодера при поступлении на его вход произвольной последовательности информационных символов, например: 1110000….. На этом примере поясним, почему рассматриваемый метод кодирования называется сверточным. Построив для заданной входной последовательности таблицу, аналогичную таблице 1, найдем, что соответствующая кодовая последовательность на выходе кодера будет иметь вид 11 01 10 01 11 00 00 00 (4). Эту выходную последовательность (4) можно также определить и другим способом, а именно на основе следующей формулы
формула (5) является дискретным аналогом известной формулы
представляющей сигнал В отличие от (6) в (5) сигналы на выходе и входе кодера рассматриваются не при непрерывном изменении времени В (5) используются такие обозначения:
Рис. 6 а) импульсная характеристика свёрточного кодера; б) входной сигнал; в) сигнал г) сигнал
график функции график функции
На рис. 6, а изображена импульсная характеристика На рис. 6, б изображен входной сигнал На рис. 6, в изображен сигнал Аналогично, график сигнала
По формуле (7) найдем значения сигнала При вычислении значений вначале определяем обычную сумму для (5), а затем - значение этой суммы по модулю 2. Так,
где функция Из этих рисунков видно, что обе функции
для Теперь нужно определить значение этой суммы по модулю 2 1 (mod 2)=1. Итак, окончательное значение Значение
Кривая При значении Таблица 2.
В таблице 2 представлены кодовые символы, когда на вход кодера поступает информационная последовательность 111000. Сравнивая кодовую последовательность, представленную этой таблицей с последовательностью (4) видим, что они идентичны. Но кодовая последовательность в таблице 2 получена на основе формулы (5), которая является дискретной сверткой импульсной характеристики кодера с входной последовательностью информационных символов. Отсюда и появилось название «сверточный кодер» для кодера, изображенного на рис. 1; а по названию кодера стали называть и сам метод кодирования- « cверточное кодирование».
12 |



 На рис. 1 изображен простейший двоичный сверточный кодер, в состав которого входит регистр сдвига, состоящий из трех ячеек (1, 2 и 3), и два сумматора по модулю 2, соединенных с соответствующими ячейками регистра сдвига.
На рис. 1 изображен простейший двоичный сверточный кодер, в состав которого входит регистр сдвига, состоящий из трех ячеек (1, 2 и 3), и два сумматора по модулю 2, соединенных с соответствующими ячейками регистра сдвига.
 , которые рассматривали раньше, характеризуются двумя целыми числами
, которые рассматривали раньше, характеризуются двумя целыми числами  , где:
, где: - количество информационных символов, поступающих на вход кодера в виде информационного блока;
- количество информационных символов, поступающих на вход кодера в виде информационного блока; - количество кодовых символов, поступающих с выхода кодера в виде кодового блока.
- количество кодовых символов, поступающих с выхода кодера в виде кодового блока. называется степенью кодирования [1] и является мерой добавленной избыточности. Информационные символы, поступающие на вход сверточного кодера, а также и кодовые символы с выхода кодера не делятся на блоки, как это было раньше, то есть сверточный код является непрерывным кодом.
называется степенью кодирования [1] и является мерой добавленной избыточности. Информационные символы, поступающие на вход сверточного кодера, а также и кодовые символы с выхода кодера не делятся на блоки, как это было раньше, то есть сверточный код является непрерывным кодом. Смысл этих чисел (параметров) следующий:
Смысл этих чисел (параметров) следующий: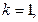 то
то  и отношение
и отношение 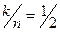 здесь также имеет смысл степени кодирования [1], как и для блочного кода. В других источниках, например, в [2] отношение
здесь также имеет смысл степени кодирования [1], как и для блочного кода. В других источниках, например, в [2] отношение  обозначают, как
обозначают, как  и называют скоростью. На практике
и называют скоростью. На практике  и
и  - это небольшие целые числа.
- это небольшие целые числа. т.е. степень кодирования (или скорость) равна
т.е. степень кодирования (или скорость) равна  .
.
 т.е. степень кодирования (или скорость) равна
т.е. степень кодирования (или скорость) равна 

 , указывающее число разрядов (ячеек) в кодирующем регистре сдвига, в которых находятся
, указывающее число разрядов (ячеек) в кодирующем регистре сдвига, в которых находятся  и эта величина означает, что поступивший на вход регистра символ на протяжении трех тактовых интервалов входного сигнала будет оказывать влияние на формируемые выходные (т.е. кодовые) символы. Таким образом, действие одного информационного символа, поступившего на вход кодера, ограничено тремя тактовыми интервалами, т.е. от момента поступления символа на вход первой ячейки регистра до момента его выхода из регистра.
и эта величина означает, что поступивший на вход регистра символ на протяжении трех тактовых интервалов входного сигнала будет оказывать влияние на формируемые выходные (т.е. кодовые) символы. Таким образом, действие одного информационного символа, поступившего на вход кодера, ограничено тремя тактовыми интервалами, т.е. от момента поступления символа на вход первой ячейки регистра до момента его выхода из регистра. ,
,  где
где 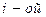 позиции вектора означает, что разряд с номером
позиции вектора означает, что разряд с номером  связан с сумматором, а нуль (0) означает, что связи между разрядом с номером
связан с сумматором, а нуль (0) означает, что связи между разрядом с номером  для верхнего сумматора и вектор связи
для верхнего сумматора и вектор связи  для нижнего сумматора. С учетом сказанного эти векторы связи будут иметь вид
для нижнего сумматора. С учетом сказанного эти векторы связи будут иметь вид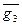 = 1 1 1 (2)
= 1 1 1 (2)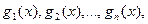 где
где  имеют порядок
имеют порядок  или меньше. Они описывают связь между разрядами регистра сдвига и соответствующими сумматорами практически так, как и векторы связи
или меньше. Они описывают связь между разрядами регистра сдвига и соответствующими сумматорами практически так, как и векторы связи  . В зависимости от того, имеется ли связь между соответствующими разрядами регистра сдвига и сумматором, в каждом слагаемом полинома коэффициенты принимают только два значения 1 или 0. Для кодера рис. 1 полиномиальные генераторы будут иметь следующий вид
. В зависимости от того, имеется ли связь между соответствующими разрядами регистра сдвига и сумматором, в каждом слагаемом полинома коэффициенты принимают только два значения 1 или 0. Для кодера рис. 1 полиномиальные генераторы будут иметь следующий вид (3).
(3).

 соответствующий кодовым символам на выходе кодера, можно определить следующим образом. Сначала найдем произведения
соответствующий кодовым символам на выходе кодера, можно определить следующим образом. Сначала найдем произведения 


 .
.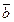 кодовых символов определяется двойными коэффициентами в круглых скобках полинома
кодовых символов определяется двойными коэффициентами в круглых скобках полинома  и
и 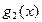 общего полиномиального множителя степени не менее единицы.
общего полиномиального множителя степени не менее единицы. =1+
=1+  ,
, 



 линейной цепи», которая является реакцией цепи на
линейной цепи», которая является реакцией цепи на  импульс).
импульс).
 величина тактового интервала для входного сигнала;
величина тактового интервала для входного сигнала; - величина тактового интервала для выходного сигнала.
- величина тактового интервала для выходного сигнала. (на выходе) в два раза меньше, чем длительность тактового интервала
(на выходе) в два раза меньше, чем длительность тактового интервала  (на входе). На рис. 5в изображена импульсная характеристика кодера – реакция на единичный символ, подаваемый на вход кодера. Входной сигнал, соответствующий этому единичному символу, представлен на рис. 5а. На всех трех рис. 5а,б,в по горизонтальной оси откладываются значения двух величин: непрерывного времени
(на входе). На рис. 5в изображена импульсная характеристика кодера – реакция на единичный символ, подаваемый на вход кодера. Входной сигнал, соответствующий этому единичному символу, представлен на рис. 5а. На всех трех рис. 5а,б,в по горизонтальной оси откладываются значения двух величин: непрерывного времени  и параметра
и параметра  и обозначает номер тактового интервала на выходе кодера длительностью
и обозначает номер тактового интервала на выходе кодера длительностью  . Значение времени
. Значение времени  удобно выбрать в середине тактового интервала, обозначенного через
удобно выбрать в середине тактового интервала, обозначенного через 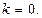 Значения, которые параметр
Значения, которые параметр 
 причем, на интервале
причем, на интервале  этот сигнал имеет форму прямоугольного импульса с амплитудой 1, а на интервале
этот сигнал имеет форму прямоугольного импульса с амплитудой 1, а на интервале  этот сигнал равен нулю.
этот сигнал равен нулю. (5),
(5), (6),
(6),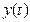 на выходе линейной цепи с импульсной характеристикой
на выходе линейной цепи с импульсной характеристикой  .
. в (6);
в (6);

 ;
; .
. ; этот параметр
; этот параметр  - значение импульсной характеристики кодера на
- значение импульсной характеристики кодера на  интервале длительностью
интервале длительностью  );
); путем зеркального отображения этого графика относительно вертикальной оси, проходящей через середину интервала
путем зеркального отображения этого графика относительно вертикальной оси, проходящей через середину интервала  (рис.6);
(рис.6); - символ суммирования в (5) является аналогом символа интегрирования
- символ суммирования в (5) является аналогом символа интегрирования  в (6); при этом суммирование в (5) осуществляется по модулю 2.
в (6); при этом суммирование в (5) осуществляется по модулю 2. . На рис. 6г изображен сигнал
. На рис. 6г изображен сигнал  , равный сигналу
, равный сигналу  . График этого сигнала
. График этого сигнала  при
при  и
и  ) в формуле (5) можно изменить пределы суммирования, т.е. бесконечные пределы заменить на конечные
) в формуле (5) можно изменить пределы суммирования, т.е. бесконечные пределы заменить на конечные (7)
(7) вычисляется согласно (5) при
вычисляется согласно (5) при  ,
, ,
, соответствующие произведения равны 0 и, таким образом, при
соответствующие произведения равны 0 и, таким образом, при  .
. вычисляется при
вычисляется при 
 ), где обе кривые одновременно отличаются от нуля и поэтому снова окончательное значение
), где обе кривые одновременно отличаются от нуля и поэтому снова окончательное значение  .
. имеем только два тактовых интервала (это
имеем только два тактовых интервала (это 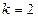 ), на которых обе функции
), на которых обе функции  не равны 0. Поэтому обычная сумма
не равны 0. Поэтому обычная сумма  будет равна 2, но так как 2(mod 2)=0, то
будет равна 2, но так как 2(mod 2)=0, то 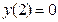 . Повторяя эту процедуру вычислений
. Повторяя эту процедуру вычислений  найдем все остальные значения
найдем все остальные значения