ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение критического пути
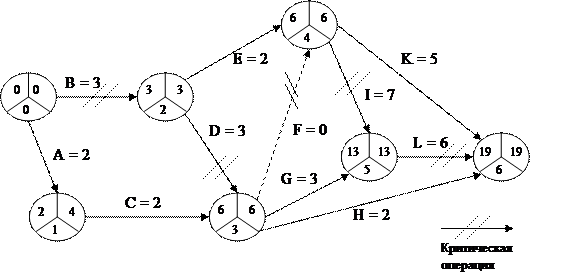
Критический путь определяет непрерывную последовательность критических операций, связывающих начальное и завершающее события сети. Другими словами, критический путь задает все критические операции проекта. Метод определения такого пути проиллюстрируем на следующем примере. Графически события изображаются кружками, разделенными на три равных сегмента (радиусами под углом в 120°); работы изображаются сплошными линиями со стрелками на конце, ориентированными слева направо; фиктивные работы изображаются пунктирными линиями со стрелками на конце, ориентированными слева направо. Пример 2. Рассмотрим сетевую модель, показанную на Рис. 5, с исходным событием 0 и завершающим событием 6. Оценки времени, необходимого для выполнения каждой операции и обозначения операций, даны у стрелок.
Рис. 5 Расчет критического пути включает два этапа. Первый этап называется прямым проходом. Вычисления начинаются с начального события и продолжаются до тех пор, пока не будет достигнуто завершающее событие всей сети. Для каждого события j вычисляется одно число На втором этапе, называемом обратным проходом, вычисления начинаются с завершающего события сети и продолжаются, пока не будет достигнуто начальное событие. Для каждого события i вычисляется число Первый этап Если принять Применительно к Рис. 5 вычисления начинаются с
На этом вычисления первого этапа заканчиваются. Второй этапначинается с завершающего события сети, для которого полагаем
Таким образом, вычисления при обратном проходе закончены.
Теперь, используя результаты вычислений первого и второго этапа, можно определить операции критического пути. Операция
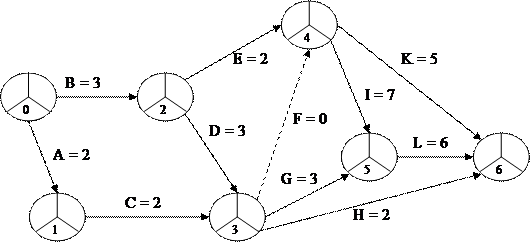
По существу, эти условия означают, что между ранним сроком начала (окончания) и поздним сроком начала (окончания) критической операции запас времени отсутствует. В сетевой модели это отражается в том, что для критических операций числа, проставленные у начальных и конечных событий, совпадают, а разность между числом у конечного события и числом у начального события равна продолжительности соответствующей операции. На Рис. 6 критический путь включает операции {B, D, F, I, L}. Критический путь определяет кратчайшую возможность всего проекта в целом. Заметим, что операции (2, 4), (3, 5), (3, 6) и (4, 6) удовлетворяют условиям (1) и (2), но не условию (3). Поэтому они не являются критическими. Отметим также, что критический путь представляет собой непрерывную цепочку операций, соединяющую исходное событие сети с завершающим.
Рис. 6
|



 , представляющее ранний срок его наступления (ранний срок окончания всех операций, входящих в событие j; ранний срок начала всех операций, выходящих из события j).
, представляющее ранний срок его наступления (ранний срок окончания всех операций, входящих в событие j; ранний срок начала всех операций, выходящих из события j). , представляющее поздний срок его наступления (поздний срок окончания всех операций, входящих в событие i, поздний срок начала всех операций, выходящих из события i).
, представляющее поздний срок его наступления (поздний срок окончания всех операций, входящих в событие i, поздний срок начала всех операций, выходящих из события i). , т.е. считать, что номер исходного события сети равен нулю, то при расчете сети полагаем
, т.е. считать, что номер исходного события сети равен нулю, то при расчете сети полагаем  . Обозначим символом
. Обозначим символом  (Duration) продолжительность операции
(Duration) продолжительность операции  . Тогда вычисления при прямом проходе выполняются по формуле
. Тогда вычисления при прямом проходе выполняются по формуле  , где max берется по всем операциям, завершающимся j-ом событии. Следовательно, чтобы вычислить
, где max берется по всем операциям, завершающимся j-ом событии. Следовательно, чтобы вычислить  начальных событий всех операций
начальных событий всех операций 

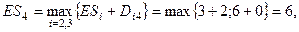
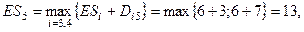
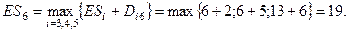
 , где n – завершающее событие. Затем, для любого события i
, где n – завершающее событие. Затем, для любого события i  , где min берется по всем операциям, выходящим из i-го события. Далее получим:
, где min берется по всем операциям, выходящим из i-го события. Далее получим:
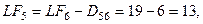
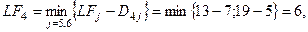
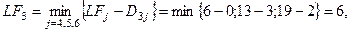
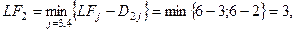
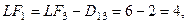
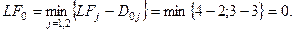
 (1)
(1) (2)
(2)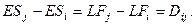 (3)
(3)