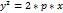ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение. Уранением линии
называеться соотношение f([)=y между координатами точек составляющих эту линию. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу • А = С = 0, В ≠0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Уравнение прямой по точке и вектору нормали Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0. Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.
39.Уравнение прямой, проходящей через 2 точки . Уравнение прямой , проходящей по точке и угловому коэффициенту
Y= Y=kx+b k-угловой коэф. Наклона k = tgα b)Ax + By + C = 0 Можно представить в виде : y = - (a/b)x – (c/b) Где к=-(a/b) ; b=-(c/b)
Ур-е прямой по точке и направляющему вектору. Ур-е прямой в отрезках. А)Каждый ненулевой вектор a = ( A B)-
41. Нормальное уравнение прямой: Если обе части уравнения A*x + B*x +C=0 уножить на
Знак необходимо выбирать так чтобы µС<0. p-длина перпендикулярна опущенного из начала координат на прямую α- < образов. этим перпендикуляром с полож. направл. оси ОХ. Угол между прямыми на плоскости Опр: Если заданы 2 прямые y1=k1*x+b1 ; y2=k2*x+b2, то острый угол будет определяться
Прямые параллельны, если k1=k2 Прямые перпендикулярны , если 1+k1*k2=0, следовательно 42. Уравнение прямой проходящей через данную точку перпендикулярно данной прямой: Опр: Прямая проходящая через точку М1 (х1;у2) и перпендикулярно прямой y=kx +b может быть представлена
Расстояние от точки до прямой: Т) Если задана точка M(x0 ; y0), то расстояние до прямой Ax+By+C=0, то рассто яние определено:
Уравнение окружности и эллипсиса
Если a=b , то уравнение окружности.
Уравнение гиперболы Опр: Гиперболой называется множество точек плоскости для которых модель разности расстояний от двух данных точек, называемыми фокусами, есть величина постоянная ,меньшая чем расстояние между фокусами.
I r1 – r2 I = const < 2c Гипербола имеет асимптоты e= Опр: Две прямые перепендикулярные действительной оси гиперболы Х и расположенные симметрично относительно центра на расстоянии а / e называется директрисами гиперболы.
Уравнение параболы Опр: Параболой называется множество точек плоскости каждой из которых находится на одинаковом расстоянии от данной точки ,называемых фокусом ,и прямой, называемой директрисой и не проходящей через фокус. Асимптот нет. р-параметр.
эксцентриситет = е=1
|



 (3, -1).
(3, -1). = y-y1=
= y-y1=  * (y1-y2)
* (y1-y2) + y1 * (
+ y1 * (  , компоненты которого удовлетворяют условию
, компоненты которого удовлетворяют условию +
+  = 0 , назыв. Направ. Вектором прямой Ax + Bx + C = 0
= 0 , назыв. Направ. Вектором прямой Ax + Bx + C = 0 -
-  y = 1 =
y = 1 =  +
+  , где a= -
, где a= -  ; b = -
; b = - 
 , которое называется нормирующим множетелем, то получим следущее уравнение
, которое называется нормирующим множетелем, то получим следущее уравнение -нормальное уравнение прямой
-нормальное уравнение прямой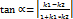
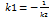
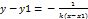
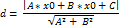
 x1 и y2- точка пересечения прямой опущенной из точки М с прямой.
x1 и y2- точка пересечения прямой опущенной из точки М с прямой.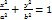 уравнение эллипса
уравнение эллипса уравнение мнимого эллипса
уравнение мнимого эллипса