ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Распределенные составные коммутаторы

Предыдущая 46 47 48 49 50 51 525354 55 56 57 58 59 60 61 Следующая

Рассмотренные выше коммутаторы представляют собой законченные устройства. Альтернативный способ построения составных коммутаторов заключается в следующем. Составной коммутатор строится из коммутаторов с v+1 входом и v+1выходом, v ≥ 2. При этом один вход каждого составляющего коммутатора служат входом и выходом составного коммутатора. Полагается, что к каждому простому коммутатору подключаются процессор и память, образуя вместе с составляющим коммутатором вычислительный модуль с v каналами для соединения с себе подобными.

Свободные vвходов и vвыходов каждого ВМ соединяются линиями «точка-точка» с входами и выходами других ВМ, образуя граф межмодульных связей. Построенные таким образом составные коммутаторы называются распределенными, в отличие от рассмотренных ранее, которые называются сосредоточенными.

Рис. 5.23. Различные топологии графа межмодульных связей

С точки зрения простоты организации передач данных между вычислительными модулями наиболее подходящий граф межмодульных связей – полный. При полном графе каждая пара ВМ имеет хотя бы одну линию связи. Однако в большинстве случаев связать каждую пару ВМ отдельным каналом связи не представляется возможным, что порождает проблему выбора графа межмодульных связей.

Отсутствие линий связи между ВМ приводит к тому, что обмен данными между ними выполняется через цепочки транзитных ВМ. Это требует определения трасс передачи данных, что является трудоемкой задачей теории графов. Очевидно, наличие транзитных передач отрицательно сказывается на времени передачи информации. Кроме этого, ограничивается число информационных обменов, которые могут проходить одновременно. Граф межмодульных связей должен выбираться исходя из минимизации времени выполнения межмодульных обменов и максимизации числа одновременно выполняемых обменов.

При выборе графа межмодульных связей важную роль играет учет отказов и восстановлений ВМ и линий связи. В каждый момент времени совокупность исправных ВМ и линий определяет существующий граф межмодульных связей. Этот граф может быть как связным, так и несвязным, состоящим из нескольких компонент связности. Так как решение параллельной задачи подразумевает обмен данными, то выбор графа должен производиться исходя из максимального сохранения связности при выходах из строя ВМ и линий.

Количество необходимых транзитных передач определяется расстоянием между вершинами графа межмодульных связей, соответствующих передающему и принимающему ВМ. Под расстоянием между вершинами графа понимается количество ребер кратчайшего пути между этими вершинами. Расстояние между максимально удаленными вершинами называетсядиаметром графа. Диаметр графа определяет максимально необходимое число транзитных передач.

В качестве показателя, оценивающего среднюю длину транзитного пути, используется средний диаметр графа, под которым понимается математическое ожидание расстояния между вершинами при равновероятном выборе пар вершин.

Очевидно, что минимизация диаметра и среднего диаметра графа межмодульных связей ведет к сокращению числа транзитных передач и, следовательно, к увеличению производительности коммуникационной среды.

Заметим, что все основные свойства графа межмодульных связей определяются его топологией. Варианты наиболее часто используемых топологий представлены на рис. 5.23.

Кроме перечисленных, важной характеристикой графа межмодульных связей является его вектор-функция структурной живучести. Вектор-функция структурной живучести графа представляет собой множество { p₁ , p₂ ,…, p_i ,…, p_N }, где N – число вершин графа.

При заданных значениях коэффициентов готовности ВМ и линий связи координата i вектор-функции задает вероятность p_i существования в графе межмодульных связей компоненты связности, включающей не менее i вершин.

Для вычисления координат вектор-функции структурной живучеститребуется проведение статистических экспериментов. Ряд экспериментальных исследований показал, что минимизация диаметра и среднего диаметра является необходимым условием максимизации координат вектор-функции структурной живучести.

Таким образом, выбор графа межмодульных связей для ВС с заданными числом ВМ N и числом линий связи каждого ВМ v может быть сведен к построению графа из Nвершин со степенями v, имеющего минимальные диаметр и средний диаметр. Однако построение такого графа является сложной задачей для большого числа вершин. Поэтому на практике часто используются графы межмодульных связей, конструируемые на основе гиперкубов («линейка», «решетка», «куб») в булевом и евклидовом пространствах.

Управление коммутаторами

Для передачи данных может использоваться метод коммутации каналов или коммутации пакетов.

При коммутации каналов (circuit switching) перед передачей данных устанавливается соединение между отправителем и получателем. Сами данные передаются только по установленному соединению. При этом может быть передан произвольный объем данных. После завершения передачи данных соединение разрушается.

При коммутации пакетов (store-and-forward switching) передаваемые данные оформляются в виде пакетов, содержащих, как правило, заголовок (head), сами данные и концевик (tail). Для удобства буферизации пакеты имеют один и тот же размер, передаваемые данные либо нарезаются на множество пакетов, либо целиком помещаются в один пакет.

Коммутация пакетов требует полного приема пакета во входной буфер коммутатора. Предполагается, что каждый вход каждого составляющего простого коммутатора имеет очередь буферов.

После приема пакета в очередь на основании маршрутной информации, содержащейся в заголовке пакета, алгоритм маршрутизации определяет выход коммутатора, через который должен быть передан данный пакет. Если требуемый выход простого коммутатора занят, пакет ожидает в буферной очереди. И так вплоть до достижения требуемого выхода составного коммутатора.

Временное хранение пакетов в буферных очередях значительно облегчает поиск маршрутов и увеличивает гибкость алгоритма маршрутизации. С другой стороны, многократные запоминания в промежуточных коммутаторах могут значительно увеличить время передачи пакета.

При коммутации каналов передаваемые данные сообщения также могут оформляться в виде пакетов. Для установления маршрута используется заголовок сообщения, что позволяет избежать приема всего пакета во входной буфер коммутатора. Заголовок передается от входа к выходу составного коммутатора, прокладывая маршрут для данных. Маршрут остается занятым на время передачи данных (пакета данных), что может привести к временным блокировкам других обменов. С другой стороны, после установления маршрута передача данных осуществляется без задержек.

Прокладывание маршрутов во время передачи заголовка и закрепление каналов на время передачи пакетов аналогичны ходам, которые проделывает червь. По этой причине указанный способ передачи данных получил название «wormhole routing» - «червячная маршрутизация».

Порядок соединения входа составного коммутатора с требуемым выходом (составление маршрута) определяется тем или иным алгоритмом маршрутизации, который выполняется блоком управления коммутатора. Блок управления коммутатора для каждого поступающего пакета данных формирует последовательность управляющих чисел d₁, d₂,…, d_N, где N – число каскадов. Управляющие числа подаются на входы соответствующих простых коммутаторов (см. рис. 5.19).

Основной задачей алгоритмов маршрутизации является нахождение, по возможности, кратчайшего пути между отправителем и получателем данных.

Алгоритмы маршрутизации могут быть детерминированными, адаптивными и частично адаптивными. Детерминированные алгоритмы, используя известный граф связей составного коммутатора, устанавливают статическую систему маршрутов, которая не может быть изменена во время работы коммутатора. При всей простоте детерминированной схемы маршрутизации ее применение сильно затрудняется сбоями и отказами простых коммутаторов и линий связи. Кроме этого, новый маршрут часто прокладывается при ранее установленных соединениях, т.е. некоторые каналы могут быть занятыми.

Адаптивные алгоритмы способны учитывать занятость и отказы простых коммутаторов и линий связи, но, как правило, имеют высокую сложность. Частично адаптивные алгоритмы функционируют как детерминированные при малой интенсивности потоков данных и отсутствия конфликтов. При обнаружении конфликтов для их разрешения осуществляется переход на адаптивную схему маршрутизации.

Любой алгоритм маршрутизации реализуется как система процессов, манипулирующих с буферами для приема и передачи данных (буферным пулом). Поскольку число буферов ограничено, может возникнуть проблема блокировок – так называемых дедлоков (deadlock). Проиллюстрируем данную проблему на следующем примере.

Пусть имеется общий буферный пул. Когда алгоритм маршрутизации нуждается в буфере, он запрашивает любой буфер из пула. Если свободного буфера нет, алгоритм останавливается в ожидании буфера.

Дедлок при таком алгоритме маршрутизации возникнет, если граф межмодульных связейимеет хотя бы один цикл. В самом деле, пусть в каждом простом коммутаторе, входящем в некоторый цикл графа, буферный пул заполнен сообщениями, адресованными следующему за этим коммутатором в цикле. Возникла ситуация, когда все коммутаторы цикла, не имея свободного буфера для приема сообщения, вошли в состояние бесконечного ожидания, т.е. образовался дедлок.

При коммутации каналов для предотвращения дедлоков следует избегать циклических топологий составного коммутатора и схем маршрутизации, допускающих циклические маршруты.

При коммутации пакетов для борьбы с дедлоками используется техника структурирования буферного пула. Рассмотрим два основных способа такого структурирования.

Буферный пул может структурироваться по линиям связей. Каждый буфер ассоциируется с определенной линией связи, при этом в буфере могут размещаться только те пакеты, которые предназначены для передачи по ассоциированной с буфером линией связи.

Для составления бездедлоковой схемы маршрутизации производятся следующие преобразования.

1. Каждое неориентированное (т.е. двунаправленное) ребро графа межмодульных связей заменяется двумя противоположно ориентированными ребрами.

2. Производится разбиение графа на множество ориентированных подграфов, при этом каждое ребро может принадлежать одному и только одному подграфу, а вершина может входить в произвольное число подграфов.

3. При составлении маршрутов фиксируется порядок прохождения подграфов – составляется граф зависимости. Граф зависимости не должен содержать циклов, т.е. при маршрутизации пакета не должны допускаться повторные заходы в пройденные подграфы.

Если существует разбиение графа межмодульных связей на ациклические ориентированные подграфы, и при любом маршруте любая пара подграфов проходится в одном и том же порядке, то маршрутизация будет бездедлоковой. Данная схема маршрутизации получила название маршрутизации с ациклическим графом зависимости.

Основным недостатком описанного способа является то, что маршрутизация с ациклическим графом зависимости не всегда позволяет использовать кратчайшие маршруты передачи данных. Например, известную топологию «конверт» (рис. 5.23-ж) можно разложить на ациклические подграфы так, как показано на рис. 5.24.

Для любого возможного маршрута фиксируем порядок прохождения – сначала подграф 1, затем – подграф 2. На рис. 5.24 отмечены две точки, минимальное расстояние между которыми равно 2, но из-за зафиксированного порядка прохождения подграфов реальное расстояние будет равно 6.

Простейшей реализацией способа структурирования буферного пула по линиям связи является алгоритм «вверх-вниз» (up-down). Из всех вершин графа межмодульных связей выбирается одна, в дальнейшем называемая корневой. Из корневой вершины строится нисходящее покрывающее дерево, включающее все вершины графа, а также обратное ему восходящее покрывающее дерево. Заметим, что дерево – принципиально ациклическая топология.

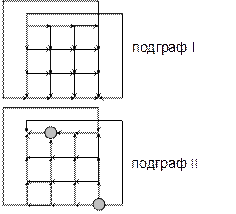
Рис. 5.24. Разложение на ациклические подграфы графа с топологией «конверт»

Алгоритм маршрутизации «вверх-вниз» заключается в следующем. Пакет данных от отправителя сначала направляется по восходящему дереву к корневой вершине. Если получатель не находится на пути следования по восходящему дереву, пакет достигает корневой вершины. Далее пакет направляется по нисходящему дереву от корневой вершины к получателю. Маршрутизация по данному алгоритму является бездедлоковой, однако почти все маршруты имеют длину, превосходящую минимально необходимую.

Другим способом структуризации буферного пула является структуризация по расстояниям(или по числу пройденных перегонов). В данном способе буферный пул является общим для всех пакетов, но при этом буферы разбиваются на классы с, по крайней мере, одним буфером в каждом классе. Число классов равно диаметру графа плюс 1.

Пакеты помечаются числом транзитных передач (пройденных перегонов), которым они подверглись. При порождении пакета, он помечается нулем. Значение отметки задает класс пакета. Пакет класса nможет размещаться только в буферах классов от 0 до n, но не выше. При этом каждый пакет будет ожидать только в том случае, когда буфер занят пакетом, находящимся ближе к своему получателю, чем рассматриваемый. Поскольку маршруты конечны, то циклическое ожидание невозможно, следовательно, данный способ маршрутизации – бездедлоковый.

Несмотря на то, что структуризация буферного пула по расстояниям позволяет использовать кратчайшие маршруты между отправителем и получателем, указанный способ обладает существенным недостатком, снижающим производительность составного коммутатора. Дело в том, что указанный алгоритм требует наличия в передающем промежуточном коммутаторе информации о состоянии буферного пула в принимающем коммутаторе. Промежуточные коммутаторы обмениваются информацией о состоянии буферного пула путем передачи служебных пакетов «запрос-ответ», что, очевидно, создает дополнительный управляющий трафик и увеличивает задержки в коммуникационной среде.

Предыдущая 46 47 48 49 50 51 525354 55 56 57 58 59 60 61 Следующая