 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Зависимые и независимые события
Начнём с независимых событий. События являются независимыми, если вероятность наступления любого из них не зависит от появления/непоявления остальных событий рассматриваемого множества (во всех возможных комбинациях). Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событий А и В равна произведению вероятностей этих событий: Р(АВ) = Р(А) × Р(В) Вернёмся к простейшему примеру 1-го урока, в котором подбрасываются две монеты и следующим событиям:
Найдём вероятность события А1А2 (на 1-й монете появится орёл и на 2-й монете появится орёл – вспоминаем, как читается произведение событий!). Вероятность выпадения орла на одной монете никак не зависит от результата броска другой монеты, следовательно, события А1 и А2 независимы. По теореме умножения вероятностей независимых событий: Р(А1А2) = Р(А1) × Р(А2) =
Заметьте, что события Теорема умножения очевидным образом распространяется и на большее количество независимых событий, так, например, если события А, В, С независимы, то вероятность их совместного наступления равна: Р(АВС ) = Р(А) × Р(В)×Р(С). Задача 3 В каждом из трех ящиков имеется по 10 деталей. В первом ящике 8 стандартных деталей, во втором – 7, в третьем – 9. Из каждого ящика наудачу извлекают по одной детали. Найти вероятность того, что все детали окажутся стандартными. Решение: вероятность извлечения стандартной или нестандартной детали из любого ящика не зависит от того, какие детали будут извлечены из других ящиков, поэтому в задаче речь идёт о независимых событиях. Рассмотрим следующие независимые события: S1 – из 1-го ящика извлечена стандартная деталь; S2 – из 2-го ящика извлечена стандартная деталь; S3 – из 3-го ящика извлечена стандартная деталь. По классическому определению: Р(S1) = Интересующее нас событие (из 1-го ящика будет извлечена стандартная деталь и из 2-го стандартная и из 3-го стандартная) выражается произведением S1S2 S3 . По теореме умножения вероятностей независимых событий: Р(S1S2 S3) = Р(S1) × Р(S2) × Р(S3) = 0,8 × 0,7 × 0,9 = 0,504 – вероятность того, что из 3-х ящиков будет извлечено по одной стандартной детали. Ответ: вероятность того, что все детали окажутся стандартными, равна 0,504 Задача 4(для самостоятельного решения) В трех урнах имеется по 6 белых и по 4 черных шара. Из каждой урны извлекают наудачу по одному шару. Найти вероятность того, что: а) все три шара будут белыми; б) все три шара будут одного цвета. Опираясь на полученную информацию, догадайтесь, как разобраться с пунктом «бэ». Примерный образец решения оформлен в академичном стиле с подробной росписью всех событий дан в конце урока. Зависимые события. Событие Х называют зависимым, если его вероятность Р(Х) зависит от одного или большего количества событий, которые уже произошли. За примерами далеко ходить не надо – достаточно дойти до ближайшего магазина: Х – завтра в 19.00 в продаже будет свежий хлеб. Вероятность этого события зависит от множества других событий: завезут ли завтра свежий хлеб, раскупят ли его до 7 вечера или нет и т.д. В зависимости от различных обстоятельств данное событие может быть как достоверным Р(Х) = 1, так и невозможным Р(Х) = 0. Таким образом, событие Х является зависимым. Другой пример, В – на экзамене студенту достанется простой билет. Если идти не самым первым, то событие В будет зависимым, поскольку его вероятность Р(В) будет зависеть от того, какие билеты уже вытянули однокурсники. |



 – в результате броска на 1-й монете выпадет орёл;
– в результате броска на 1-й монете выпадет орёл; – в результате броска на 2-й монете выпадет орёл.
– в результате броска на 2-й монете выпадет орёл. ×
×  =
= 
 =
=  ×
×  =
=  =
=  ×
×  =
=  =
=  ,
, 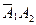 ,
, 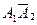 ,
,  образуют полную группу и сумма их вероятностей равна единице:
образуют полную группу и сумма их вероятностей равна единице:  +
+  = 1
= 1 = 0,8; Р(S2) =
= 0,8; Р(S2) =  = 0,7; Р(S3) =
= 0,7; Р(S3) =  = 0,9; – соответствующие вероятности.
= 0,9; – соответствующие вероятности.