ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Зависимые события и условная вероятность
На предыдущем уроке (смотри выше) мы ознакомились с основными теоремами сложения и умножения вероятностей, а также научились решать типовые задачи с независимыми событиями, и сейчас последует гораздо более интересное продолжение, которое позволит не только освоить новый материал, но и, возможно, окажет практическую житейскую помощь. Кратко повторим, что такое независимость событий: события А и В являются НЕзависимыми, если вероятность любого из них не зависит от появления либо непоявления другого события. Простейший пример – подбрасывание двух монет. Вероятность выпадения орла либо решки на одной монете никак не зависит от результата броска другой монеты. Понятие зависимости событий вам тоже знакомо и настал черёд заняться ими вплотную. Сначала рассмотрим традиционный набор, состоящий из двух событий: событие В является зависимым, если помимо случайных факторов его вероятность зависит от появления либо непоявления события А. Вероятность события В, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В и обозначается через РА(В). При этом события А и В называют зависимыми событиями (хотя, строго говоря, зависимо только одно из них). Задача 1 Из колоды в 36 карт последовательно извлекаются 2 карты. Найти вероятность того, что вторая карта окажется червой, если до этого: а) была извлечена черва; Решение: рассмотрим событие: В – вторая карта будет червой. Совершенно понятно, что вероятность этого события зависит от того, черву или не черву вытянули ранее. а) Если сначала была извлечена черва (событие А), то в колоде осталось 35 карт, среди которых теперь находится 8 карт червовой масти. По классическому определению: РА(В) = б) Если же сначала была извлечена карта другой масти (событие Всё логично – если вероятность извлечения червы из полной колоды составляет Р(А) = Ответ: а) вероятность того, что была извлечена черва, равна Зависимых событий, разумеется, может быть и больше. Пока задача не остыла, добавим ещё одно: С– третьей картой будет извлечена черва. Предположим, что произошло событие А, а затем событие В; тогда в колоде осталось 34 карты, среди которых 7 черв. По классическому определению: РАВ(С) = Задача 2 для самостоятельного решения В конверте находится 10 лотерейных билетов, среди которых 3 выигрышных. Из конверта последовательно извлекаются билеты. Найти вероятности того, что: а) 2-й извлечённый билет будет выигрышным, если 1-й был выигрышным; Краткое решение с комментариями в конце урока. А теперь обратим внимание на один принципиально важный момент: в рассмотренных примерах требовалось найти лишь условные вероятности, при этом предыдущие события считались достоверно состоявшимися. Но ведь в действительности и они являются случайными! Так, в рассмотренной задаче извлечение червы из полной колоды – есть событие случайное, вероятность которого равна Р(А) = На практике гораздо чаще требуется отыскать вероятность совместного появления зависимых событий. Как, например, найти вероятность события А × В, состоящего в том, что из полной колоды будет извлечена черва и затем ещё одна черва? Ответ на этот вопрос даёт теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло: Р(АВ) = Р(А) × РА(В) Аналогично: Р( Вероятность события И, само собой, не нужно питать особых надежд, что из конверта с десятью лотерейными билетами (Задача 2) вы вытяните 3 выигрышных билета подряд: Р(А1А2А3) = Р(А1) × Итак, теорема умножения вероятностей зависимых событий естественным образом распространяется и на большее их количество. Задача 3 – типовая задача. В урне 4 белых и 7 черных шаров. Из урны наудачу один за другим извлекают два шара, не возвращая их обратно. Найти вероятность того, что: а) оба шара будут белыми; Обратите внимание на уточнение «не возвращая их обратно». Этот комментарий дополнительно подчёркивает тот факт, что события зависимы. Действительно, а вдруг извлечённые шары возвращают обратно? В случае возвратной выборки вероятности извлечения чёрного и белого шара меняться не будут, а в такой задаче уже следует руководствоваться теоремой умножения вероятностей НЕзависимых событий. Решение: всего в урне: 4 + 7 = 11 шаров. а) Рассмотрим события А – первый шар будет белым, В – второй шар будет белым и найдём вероятность события АВ, состоящего в том, что 1-ый шар будет белым и 2-ой белым. По классическому определению вероятности: Р(А) = По теореме умножения вероятностей зависимых событий: Р(АВ) = Р(А) × РА(В) = б) Найдём вероятность события По классическому определению: По теореме умножения вероятностей зависимых событий: Р( в) Найдём вероятность события После извлечения белого шара (с вероятностью Р(А) = По теореме умножения вероятностей зависимых событий: Р( Ответ: а) вероятность того, что оба шара будут белыми равна Данную задачу нетрудно проверить через теорему сложения вероятностей событий, образующих полную группу. Для этого найдём вероятность 4-го недостающего события: Р( События АВ,
Задача 4 для самостоятельного решения Какова вероятность того, что из колоды в 36 карт будут извлечены два туза подряд? Задача 5 для самостоятельного решения В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара. Найти вероятность того, что а) третий шар окажется белым, если до этого был извлечён черный и красный шар; Решения и ответы в конце урока. Надо сказать, что многие из рассматриваемых задач разрешимы и другим способом, но чтобы не возникло путаницы, пожалуй, вообще о нём умолчу. Решения и ответы: Задача 2: В конверте находится 10 лотерейных билетов, среди которых 3 выигрышных. Из конверта последовательно извлекаются билеты. Найти вероятности того, что: а) 2-й извлечённый билет будет выигрышным, если 1-й был выигрышным; Решение: рассмотрим события: а) Пусть событие б) Если произошли события в) Если произошли события Ответ: Задача 4: Какова вероятность того, что из колоды в 36 карт будут извлечены два туза подряд? Решение: всего: 4 туза в колоде. Рассмотрим события Задача 5: В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара. Найти вероятность того, что а) третий шар окажется белым, если до этого был извлечён черный и красный шар; Решение: всего: 6 + 5 + 4 = 15 шаров в урне. Рассмотрим следующие события: а) По условию, события б) По классическому определению: Ответ: |



 – вероятность того, что вторая карта окажется червой при условии, что до этого тоже была извлечена черва.
– вероятность того, что вторая карта окажется червой при условии, что до этого тоже была извлечена черва. ), то все 9 черв остались в колоде. По классическому определению: РА(В) =
), то все 9 черв остались в колоде. По классическому определению: РА(В) = 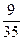 – вероятность того, что вторая карта окажется червой при условии, что до этого была извлечена карта другой масти.
– вероятность того, что вторая карта окажется червой при условии, что до этого была извлечена карта другой масти. = 0,25, то при извлечении следующей карты аналогичная вероятность изменится: в первом случае – уменьшится РА(В) =
= 0,25, то при извлечении следующей карты аналогичная вероятность изменится: в первом случае – уменьшится РА(В) =  – вероятность наступления события С при условии, что до этого были извлечены две червы.
– вероятность наступления события С при условии, что до этого были извлечены две червы. .
.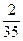 » 0,0571 – вероятность того, что из полной колоды будут извлечены 2 червы подряд.
» 0,0571 – вероятность того, что из полной колоды будут извлечены 2 червы подряд.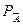 (В) =
(В) =  ×
×  » 0,1929 – вероятность того, что сначала будет извлечена карта другой масти изатем черва.
» 0,1929 – вероятность того, что сначала будет извлечена карта другой масти изатем черва. (А2) ×
(А2) ×  (А3) =
(А3) =  ×
× 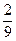 ×
×  =
=  » 0,0083.
» 0,0083. . Предположим, что белый шар извлечён, тогда в урне останется 10 шаров, среди которых 3 белых, поэтому: РА(В) =
. Предположим, что белый шар извлечён, тогда в урне останется 10 шаров, среди которых 3 белых, поэтому: РА(В) =  – вероятность того, что оба шара будут белыми.
– вероятность того, что оба шара будут белыми. , состоящего в том, что 1-ый шар будет чёрным и 2-ой чёрным
, состоящего в том, что 1-ый шар будет чёрным и 2-ой чёрным =
=  – вероятность того, что в 1-м испытании будет извлечён чёрный шар. Пусть извлечён чёрный шар, тогда в урне останется 10 шаров, среди которых 6 чёрных, следовательно:
– вероятность того, что в 1-м испытании будет извлечён чёрный шар. Пусть извлечён чёрный шар, тогда в урне останется 10 шаров, среди которых 6 чёрных, следовательно: 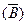 =
=  =
=  – вероятность того, что во 2-м испытании будет извлечён чёрный шар при условии, что до этого был извлечен чёрный шар.
– вероятность того, что во 2-м испытании будет извлечён чёрный шар при условии, что до этого был извлечен чёрный шар.
 (сначала будет извлечён белый шар и затем чёрный)
(сначала будет извлечён белый шар и затем чёрный) ) =
) =  – вероятность того, что во 2-м испытании будет извлечён чёрный шар при условии, что до этого был извлечен белый шар.
– вероятность того, что во 2-м испытании будет извлечён чёрный шар при условии, что до этого был извлечен белый шар. – искомая вероятность.
– искомая вероятность. ) =
) = 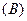 =
=  =
=  – при 1-й, 2-й, 3-ей и 4-й попытках соответственно будет извлечён выигрышный билет.
– при 1-й, 2-й, 3-ей и 4-й попытках соответственно будет извлечён выигрышный билет. состоялось. Тогда в конверте осталось 9 билетов, среди которых 2 выигрышных. По классическому определению:
состоялось. Тогда в конверте осталось 9 билетов, среди которых 2 выигрышных. По классическому определению: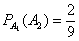 – вероятность того, что 2-й выбранный билет будет выигрышным при условии, что до этого извлечён выигрышный билет.
– вероятность того, что 2-й выбранный билет будет выигрышным при условии, что до этого извлечён выигрышный билет. , то в конверте осталось 8 билетов, среди которых 1 выигрышный. По классическому определению:
, то в конверте осталось 8 билетов, среди которых 1 выигрышный. По классическому определению: – вероятность того, что 3-й выбранный билет будет выигрышным при условии, что до этого было извлечено два выигрышных билета.
– вероятность того, что 3-й выбранный билет будет выигрышным при условии, что до этого было извлечено два выигрышных билета.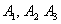 , то в конверте не осталось выигрышных билетов. По классическому определению:
, то в конверте не осталось выигрышных билетов. По классическому определению: – вероятность того, что 4-й выбранный билет будет выигрышным при условии, что до этого были извлечены три выигрышных билета.
– вероятность того, что 4-й выбранный билет будет выигрышным при условии, что до этого были извлечены три выигрышных билета.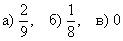
 – первой картой будет извлечён туз,
– первой картой будет извлечён туз,  – 2-й картой будет извлечён туз. По классическому определению вероятности:
– 2-й картой будет извлечён туз. По классическому определению вероятности:  . В случае осуществления события
. В случае осуществления события  – вероятность того, что 2-й картой будет извлечён туз, при условии, что до этого был извлечен туз.
– вероятность того, что 2-й картой будет извлечён туз, при условии, что до этого был извлечен туз. – вероятность того, что из колоды в 36 карт будут извлечены два туза подряд.
– вероятность того, что из колоды в 36 карт будут извлечены два туза подряд.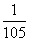
 – 3-й шар будет белым.
– 3-й шар будет белым. – вероятность того, что 3-й шар будет белым при условии, что до этого был извлечён черный и красный шар.
– вероятность того, что 3-й шар будет белым при условии, что до этого был извлечён черный и красный шар. . Предположим, что событие
. Предположим, что событие 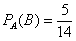 – вероятность того, что 2-й шар будет красным при условии, что 1-й был чёрным.
– вероятность того, что 2-й шар будет красным при условии, что 1-й был чёрным. – вероятность того, что первый шар окажется черным и второй – красным и третий – белым
– вероятность того, что первый шар окажется черным и второй – красным и третий – белым