ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Как определить зависимость/независимость событий?
Иногда об этом прямо сказано в условии задачи, но чаще всего приходится проводить самостоятельный анализ. Какого-то однозначного ориентира тут нет, и факт зависимости либо независимости событий вытекает из естественных логических рассуждений. Чтобы не валить всё в одну кучу, задачам на зависимые события я выделю следующий урок, а пока мы рассмотрим наиболее распространённую на практике связку теорем: Задачи на теоремы сложения вероятностей несовместных Этот тандем, по моей субъективной оценке, работает примерно в 80% задач по рассматриваемой теме. Хит хитов и самая настоящая классика теории вероятностей: Задача 5 Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,6. Найти вероятность того, что: а) только один стрелок попадёт в мишень; Решение: вероятность попадания/промаха одного стрелка, очевидно, не зависит от результативности другого стрелка. Рассмотрим события: А1 – 1-й стрелок попадёт в мишень; А2 – 2-й стрелок попадёт в мишень. По условию: Р(А1) = 0,8; Р(А2) = 0,6. Найдём вероятности противоположных событий
а) Рассмотрим событие: В – только один стрелок попадёт в мишень. Данное событие состоит в двух несовместных исходах: 1-й стрелок попадёт и2-й промахнётся
На языке алгебры событий этот факт запишется следующей формулой: В = Сначала используем теорему сложения вероятностей несовместных событий, затем – теорему умножения вероятностей независимых событий: Р(В) =Р( = 0,8 × 0,4 + 0,2 × 0,6 = 0,32 + 0,12 = 0,44 – вероятность того, что будет только одно попадание.
б) Рассмотрим событие: С – хотя бы один из стрелков попадёт в мишень.
Прежде всего, ВДУМАЕМСЯ – что значит условие «ХОТЯ БЫ ОДИН»? В данном случае это означает, что попадёт или 1-й стрелок (2-й промахнётся) или 2-й (1-й промахнётся) или оба стрелка сразу – итого 3 несовместных исхода. Способ первый: учитывая готовую вероятность предыдущего пункта, событие удобно представить в виде суммы следующих несовместных событий: попадёт кто-то один (событие В, состоящее в свою очередь из 2-х несовместных исходов) или Таким образом: C = B + D. По теореме умножения вероятностей независимых событий: P (D) = P(А1 А2) = P(А1) × P(А2) = 0,8 × 0,6 = 0,48 – вероятность того, что 1-й стрелок попадёт и 2-ой стрелок попадёт. По теореме сложения вероятностей несовместных событий: Р(C) = Р(B + D) = Р( B) + Р( D) = 0,44 + 0,48 = 0,92. – вероятность хотя бы одного попадания по мишени. Способ второй: рассмотрим противоположное событие: По теореме умножения вероятностей независимых событий: Р( В результате: Р(С) = 1 – Р(
Особое внимание обратите на второй способ – в общем случае он более рационален. Кроме того, существует альтернативный, третий путь решения, основанный на теореме, которая будет рассмотрена на следующем уроке: теореме сложения совместных событий. !Если вы знакомитесь с материалом впервые, то во избежание путаницы, следующий абзац лучше пропустить. Способ третий: события А1 и А2 совместны, а значит, их сумма А1 + А2 выражает событие «хотя бы один стрелок попадёт в мишень» (см. алгебру событий). По теореме сложения вероятностей совместных событий и теореме умножения вероятностей независимых событий: Р(А1 + А2) = Р(А1) + Р( А2) –Р(А1× А2) = Р(А1) + Р( А2) – Р(А1) × Р(А2) = = 0,8 + 0,6 – 0,8 × 0,6 = 1,4 – 0,48 = 0,92
Выполним проверку: события Р( Ответ: а) вероятность того, что только один стрелок попадёт в мишень, равна 0,44, б) вероятность того, что хотя бы один из стрелков попадёт в мишень, равна 0,92 На практике можно пользоваться любым вариантом оформления. Конечно же, намного чаще идут коротким путём, но не нужно забывать и 1-й способ – он хоть и длиннее, но зато содержательнее – в нём понятнее, что, почему и зачем складывается и умножается. Похожие задачи: Задача 6 для самостоятельного решения Для сигнализации о возгорании установлены два независимо работающих датчика. Вероятности того, что при возгорании датчик сработает, для первого и второго датчиков соответственно равны 0,5 и 0,7. Найти вероятность того, что при пожаре: а) оба датчика откажут; Здесь независимость работы устройств непосредственно прописана в условии, что, кстати, является важным уточнением. Образец решения оформлен в академичном стиле. Как быть, если в похожей задаче даны одинаковые вероятности, например, 0,9 и 0,9? Решать нужно точно так же! Задача 7 Стрелок попадает в цель с одной и той же вероятностью при каждом выстреле. Какова эта вероятность, если вероятность хотя бы одного попадания при трех выстрелах равна 0,973. Решение: обозначим через И таки распишем события: По условию С другой стороны, по теореме умножения вероятностей независимых событий: Таким образом: В результате: Ответ: 0,7 Просто и изящно.
Решения и ответы: Задача 2: В коробке 10 красных и 6 синих пуговиц. Наудачу извлекаются две пуговицы. Какова вероятность того, что они будут одноцветными? Решение:всего: 10 + 6 = 16 пуговиц в коробке. Задача 4: В трех урнах имеется по 6 белых и по 4 черных шара. Из каждой урны извлекают наудачу по одному шару. Найти вероятность того, что: а) все три шара будут белыми; б) все три шара будут одного цвета. Решение: рассмотрим события: а) Рассмотрим событие: б) Рассмотрим событие Ответ: Задача 6: Для сигнализации о возгорании установлены два независимо работающих датчика. Вероятности того, что при возгорании датчик сработает, для первого и второго датчиков соответственно равны 0,5 и 0,7. Найти вероятность того, что при пожаре: Решение:рассмотрим следующие события: а) Рассмотрим событие: б) Рассмотрим событие: в) Рассмотрим событие: Ответ: Следующий урок |



 – того, что соответствующие стрелки промахнутся:
– того, что соответствующие стрелки промахнутся: = 1 -
= 1 -  = 1 – 0,8 = 0,2;
= 1 – 0,8 = 0,2; = 1 -
= 1 -  = 1 – 0,6 = 0,4;
= 1 – 0,6 = 0,4;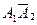 +
+ 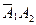
 ) × Р(
) × Р(  ) +Р(
) +Р(  ) × Р(
) × Р(  ) =
) = – оба стрелка промахнутся.
– оба стрелка промахнутся. – вероятность попадания в мишень при каждом выстреле.
– вероятность попадания в мишень при каждом выстреле. – вероятность промаха при каждом выстреле.
– вероятность промаха при каждом выстреле. – при 3-х выстрелах стрелок попадёт в мишень хотя бы один раз;
– при 3-х выстрелах стрелок попадёт в мишень хотя бы один раз; – стрелок 3 раза промахнётся.
– стрелок 3 раза промахнётся. , тогда вероятность противоположного события:
, тогда вероятность противоположного события: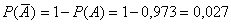
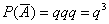
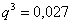
 – вероятность промаха при каждом выстреле.
– вероятность промаха при каждом выстреле. – вероятность попадания при каждом выстреле.
– вероятность попадания при каждом выстреле. способами можно извлечь 2 пуговицы из коробки;
способами можно извлечь 2 пуговицы из коробки; способами можно извлечь 2 красные пуговицы;
способами можно извлечь 2 красные пуговицы; способами можно извлечь 2 синие пуговицы.
способами можно извлечь 2 синие пуговицы. – вероятность того, что из коробки будут извлечены две красные пуговицы;
– вероятность того, что из коробки будут извлечены две красные пуговицы; – вероятность того, что из коробки будут извлечены две синие пуговицы.
– вероятность того, что из коробки будут извлечены две синие пуговицы. – вероятность того, что из коробки будут извлечены две одноцветные пуговицы.
– вероятность того, что из коробки будут извлечены две одноцветные пуговицы. – из 1-й, 2-й и 3-й урны соответственно будет извлечён белый шар. По классическому определению вероятности:
– из 1-й, 2-й и 3-й урны соответственно будет извлечён белый шар. По классическому определению вероятности: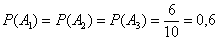
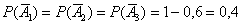
 – из каждой урны будет извлечено по 1-му белому шару.
– из каждой урны будет извлечено по 1-му белому шару. (из 1-й урны будет извлечён БШ и из 2-ой урны будет извлечён БШ и из 3-й урны будет извлечён БШ).
(из 1-й урны будет извлечён БШ и из 2-ой урны будет извлечён БШ и из 3-й урны будет извлечён БШ).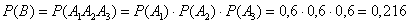
 – из каждой урны будет извлечено по 1-му чёрному шару.
– из каждой урны будет извлечено по 1-му чёрному шару.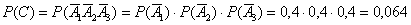
 – все три шара будут одного цвета. Данное событие состоит в двух несовместных исходах:
– все три шара будут одного цвета. Данное событие состоит в двух несовместных исходах:  (будут извлечены 3 белых или 3 чёрных шара)
(будут извлечены 3 белых или 3 чёрных шара)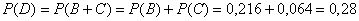
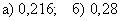
 – при возгорании сработает 1-й датчик;
– при возгорании сработает 1-й датчик; – при возгорании сработает 2-й датчик.
– при возгорании сработает 2-й датчик.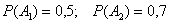
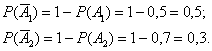
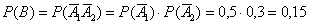
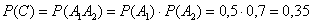
 образуют полную группу, следовательно:
образуют полную группу, следовательно: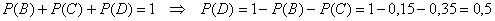
 .
.