ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Теория оптимизации кольцевого маршрута

1 234

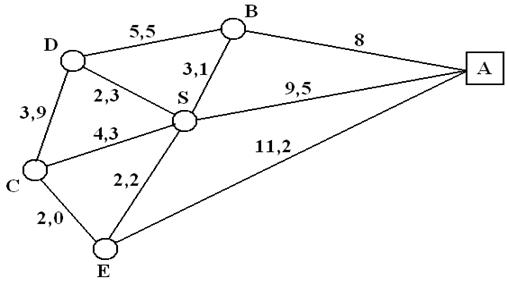
Одной из важных задач в логистике является разработка моделей транспортного обслуживанияпотребителей и поставщиков, расчет рациональных маршрутов перевозки, составление графиков доставки продукции потребителям.

Маршрутизация перевозок– это наиболее совершенный способ организации материалопотока. Маршрутизация позволяет повысить производительность транспортных средств и сократить объем запасов, хранящихся у поставщиков и потребителей.

Маршрут движения– это путь следования транспорта при выполнении перевозок. Выделяют маятниковые и кольцевые маршруты движения.

При маятниковом маршруте путь следования транспорта между пунктами неоднократно повторяется.

Кольцевой маршрут– это маршрут движения транспорта по замкнутому контуру, соединяющему несколько потребителей или поставщиков. Разновидностями кольцевого маршрута являются развозочные маршруты, сборные и сборно-развозочные.

Развозочный кольцевой маршрут– это маршрут, при котором продукция загружается у одного поставщика и развозится нескольким потребителям.

Сборный кольцевой маршрут– это маршрут движения, при котором продукция получается у нескольких поставщиков и доставляется одному потребителю.

Сборно-развозочный кольцевой маршрут– это сочетание развозочного и сборного кольцевых маршрутов.

Организация развозочного кольцевого маршрута является одной из наиболее сложных задач транспортной логистики. При его организации из одного отправного пункта (например, с оптовой базы) отправляются разные товары в несколько пунктов назначения (например, магазины розничной торговли) с последовательным их посещением. Целью задачи является поиск замкнутого маршрута с минимальной транспортной работой.

При расчете кольцевого маршрутаисходными данными являются: 1) схема размещения пункта отправки и пунктов назначения, 2) расстояния между ними, 3) объем (масса) груза поставляемого в каждый из пунктов назначения, 4) вместимость и грузоподъемность выделяемого для перевозки транспорта. Обычно выбор простого маршрута производится путем перебора всех возможных вариантов и выбора из них оптимального. Так если к расчету принимается четыре пункта (одна база и три пункта получения), то количество возможных транспортных маршрутов будет равно шести.

Например, если обозначить пункт отправки А, а пункты получения Б₁, Б₂, Б₃, то можно выбрать один из следующих шести маршрутов:

1. А - Б₁- Б₂ - Б₃ - А; 2. А - Б₁- Б₃ - Б₂ - А; 3. А-Б₂- Б₁- Б₃-А; 4. А - Б₂ - Б₃ - Б₁ - А; 5. А – Б₃ - Б₁ – Б₂- А; 6. А - Б₃ - Б₂ - Б₁- А .

В данном случае выбор производится с точки зрения минимизации суммарного расстояния пробега, так как от него зависит величина транспортных затрат.

Однако для 20 пунктов количество возможных маршрутов составляет уже около 6 млн. Поэтому на практике применяются приближенные алгоритмы и допускается возможная неоптимальность получаемых решений.

Выбор маршрута влияет на последовательность загрузки товаров на транспортное средство. Первой грузится партия для последнего пункта получения и располагается в самой дальней части кузова, а партия для первого получателя располагается последней у самого края.

Порядок выполнения работы:

1. Войти в операционную систему Windows, открыть диск с программами Programs Jailer Р, открыть папку «ЛОГИСТИКА для студентов», открыть папку «Лаб. работа 2», открыть папку своей подгруппы, скопировать указанный преподавателем файл «ЛР2-1 Лист Microsoft Excel».Открыть диск с программами Programs Jailer S, открыть папку своей группы, открыть свою папку и сохранить в ней скопированный файл под своей фамилией.

Например, файл Иванов ЛР2.xls в папке М-31 2010 г. логистика.

2. Работа выполняется в файле, который является книгой Excel и содержит два листа:

1-й лист называется «Таблица-матрица»;

2-й лист - «Расчет оптимального маршрута».

Начальным этапом выполнения лабораторной работы является расчет длины оптимального кольцевого маршрута по контрольным исходным данным.

Контрольный вариант исходных данных для апробирования методики расчета представлен на 1-м листе(рис. 1).Следующий вариант данных для расчета представлен на листе «Исходные данные» пособия – его назначает руководитель.

Рис. 1. Схема размещения пунктов потребления и расстояния между ними

Расчеты на 1-м листе «Таблица-матрица»

На 1-м листепредставлена схема размещения транспортных пунктов: пунктов потребления и расстояний между ними. На данном листе необходимо рассчитать три таблицы и определить начальный базовый маршрут (три первых пункта, имеющих max сумму по столбцу).

1.В соответствующие ячейки таблицы №1 необходимо внести основные возможные варианты «маршрутов» в виде расстояний между пунктами, используя функцию Excel «Суммирование».

Таблица №1

Таблица, определяющая все возможные близлежащие расстояния между пунктами кольцевого маршрута

От А до	От В до
В	D	S	С	Е	D	S	С	Е
	13,5	9,5	13,8	11,2	5,5	3,1	9,4	5,3
12,6	11,8	11,1	13,2	11,7	5,4	7,8	7,4	11,4
17,3	13,4	13,4	15,4	13,3	11,3	17,5	7,3	9,4
	15,1		17,4				9,3	10,0
От D до	От S до	От С до
S	С	Е	С	Е	Е
2,3	3,9	5,9	4,3	2,2	2,0
8,6	6.6	4,5	4,2	6,3	6,5
8,2	6,5	8,6	6,2

Для этого необходимо определить возможные варианты проезда из одного пункта в другой и рассчитать суммарное расстояние каждого варианта по формуле суммы, используя ячейки с данными расстояний в схеме размещения транспортных пунктов. При этом варианты проезда выбираются только те, у которых маршруты движения от пункта до пункта проходят не более чем через два промежуточных пункта. В ячейке таблицы 1 ставится «=» и по данным схемы формируется маршрут.

2.На основании данныхтаблицы №1 в таблицу №2 заносятся минимальные расстояния между пунктами схемы, используя стандартную функцию определения минимального значения из столбца данных (МИН): = МИН (число 1; число 2; ...), выбираемое из всех занесенных в столбцы таблицы №1 вариантов маршрутов. Так если из пункта А в пункт Е можно доехать тремя вариантами. Из них с помощью функции (МИН) выбирается тот, который имеет минимальное расстояние.

В ячейке расстояния между i-м и i-м пунктом ставится прочерк.

В нижней строкетаблицы №2 (Итого) определяется сумма расстояний по столбцам между i-м пунктом и остальными маршрутными пунктами.

Таблица №2

Таблица - матрица с кратчайшими расстояниями между пунктами (рассчитать

по формуле = МИН(число1;[число2];...))

	А	В	D	S	С	Е
А	▬		11,8	9,5	13,2	11,2
В		▬	5,4	3,1	7,3	5,3
D	11,8	5,4	▬	2,3	3,9	4,5
S	9,5	3,1	2,3	▬	4,2	2,2
С	13,2	7,3	3,9	4,2	▬	2,0
Е	11,2	5,3	4,5	2,2	2,0	▬
Итого	53,7	29,1	27,9	21,3	30,6	25,2

Строка полученных сумм автоматически переходит в таблицу №3, которая предназначена для определения базового маршрута.

Таблица №3

Таблица-матрица для определения базового маршрута

Суммарные расстояния и пункты по убыванию	Итоговые результаты (из таблицы № 2)
Пункт	Расстояние	53,7	29,1	27,9	21,3	30,6	25,2
А	53,7		29,1	27,9	21,3	30,6	25,2
С	30,6		29,1	27,9	21,3		25,2
В	29,1			27,9	21,3		25,2
D	27,9				21,3		25,2
Е	25,2				21,3
S	21,3

3. Таблица №3 заполняется таким образом, чтобы в столбце «Расстояние» суммы выстроились в убывающем порядке. А в столбце «Пункт» напротив каждой суммы был соответствующий ей пункт.

Последовательность заполнения таблицы№3

- строка «Итого» таблицы №2 автоматически перейдет в таблицу №3 в столбец «Итоговые результаты». Данные строки являются исходной информацией для дальнейших расчетов;

- в верхней ячейке столбца «Расстояние» по формуле = МАКС (число1; число 2; ...) определяется максимальная величина в строке колонки «Итоговые результаты»;

- с использованием функции: = Если (лог_выражение;[значение_если_истина]; [значение_если_ложь]), где истина = 0, заполняется следующая строка колонки «Итоговые результаты» таким образом, чтобы вычисленное максимальное значение стало равно 0, а остальные значения были перенесены без изменений;

- подобным образом заполнить колонку «Расстояние» и всю колонку «Итоговые результаты», при этом в колонке «Расстояние» выстраивается цепочка расстояний по убыванию;

- используя результаты расчетов таблицы №2 и таблицы №3, а также функцию: = Если (лог_выражение;[значение_если_истина]; [значение_если_ложь]), где истина = искомый пункт, заполнить колонку «Пункт», в которой выстраиваются пункты маршрута согласно суммарные значения строки «Итого» таблицы №2.

Базовый маршрутсостоит из первых трех пунктов, имеющих максимальные суммарные значения величины маршрутов столбца «Расстояния» (выделены в таблице №3 жирным шрифтом). Выбранные пункты переносятся в строку базового маршрута путем ссылки на соответствующие ячейки таблицы №3.

Базовый маршрут:

Расчеты на2-м листе «Расчет оптимального маршрута»

1.Перенести результаты, полученные в таблице №2, и базовый маршрут на 2-й лист в таблицу-матрицу, определяющую минимальные расстояния между пунктами кольцевого маршрута путем ссылок. Заполнять следует ту часть таблицы, ячейки которой свободны и не содержат нули.

Таблица-матрица, определяющая минимальные расстояния между пунктами

кольцевого маршрута

	А	В	D	S	С	Е	Итого по строкам
А	▬		11,8	9,5	13,2	11,2	53,7
В		▬	5,4	3,1	7,3	5,3	29,1
D	11,8	5,4	▬	2,3	3,9	4,5	27,9
S	9,5	3,1	2,3	▬	4,2	2,2	21,3
С	13,2	7,3	3,9	4,2	▬	2,0	30,6
Е	11,2	5,3	4,5	2,2	2,0	▬	25,2
Итого по столбцам	53,7	29,1	27,9	21,3	30,6	25,2	▬

2. Расчетная таблица №1 заполняется автоматически.

Расчетная таблица №1

	А	С	В	D	Е	S	Итого по убыванию
А	0,0	13,2	8,0	11,8	11,2	9,5	53,7
С	13,2	0,0	7,3	3,9	2,0	4,2	30,6
В	8,0	7,3	0,0	5,4	5,3	3,1	29,1
D	11,8	3,9	5,4	0,0	4,5	2,3	27,9
Е	11,2	2,0	5,3	4,5	0,0	2,2	25,2
S	9,5	4,2	за	2,3	2,2	0,0	21,3
Итого по убыванию	53,7	30,6	29,1	27,9	25,2	21,3	0,0

3.В базовый маршрут состоящий из трех пунктов первым включается пункт, который имеет следующую наибольшую сумму расстояний по столбцу после первых трех базовых (4-й по рангу из таблицы №3). При этом решается задача, между какими пунктами его следует включить. Для этого определяем размер приращения маршрута ΔL для каждой пары пунктов по формуле: ΔL₁₂ = L₁_i + L_i₂ – L₁₂,

где L – расстояние между пунктами, км;

i - индекс включаемого пункта;

1 - индекс первого пункта из пары;

2 - индекс второго пункта из пары.

Размеры приращений находятся в «Таблице для расчета приращений».

Например, если базовыми являлись пункты А, С, В, а четвертым пунктом – пункт D, то формулы расчета приращений имеют вид:

ΔAC = AD+DC-AC; ΔCB-CD + DB-CB; ΔBA = BD + DA-BA.

Пункт D размещается между пунктами, которые имеют наименьшее приращение.

Для сравнения и выбора из полученных значений приращений минимальное определяется с использованием формулы: = МИН (число1; число2; ...), которое заносится в соответствующую ячейку:

Минимальное значение равно:

В результате получаем новый маршрут из 4-х пунктов.

введение 5-го и 6-го пунктов осуществляется тем же способом.

Итогом расчетов является получения кольцевого маршрута, проходящего через все заданные пункты, имеющего минимальную длину.

Для расчета схемы следующего варианта скопируйте два расчетных листа 1-го варианта и замените исходные данные. Если все формулы верны, то результат получится автоматически.

При составлении программы расчёта кольцевого маршрута на компьютере в ячейки таблиц вставлять толькоформулы!!! функций, чтобы в дальнейшем с изменением расстояний между пунктами, полученные расчеты по каждой схеме изменялись автоматически.

1 234