 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
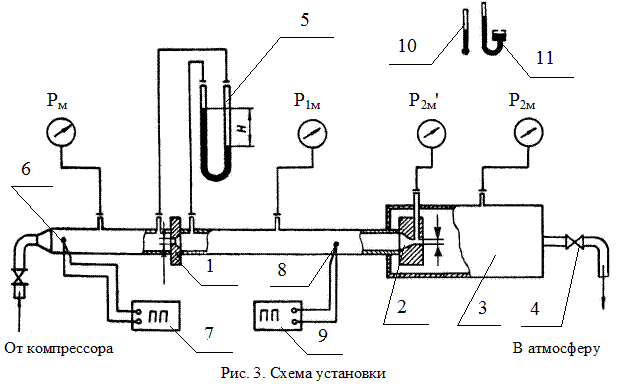
| Схема и описание установки
В камере 3 за соплом, куда происходит истечение, можно устанавливать различные давления выше барометрического путем изменения проходного сечения для воздуха с помощью вентиля 4. А затем воздух направляется в атмосферу. Сопло выполнено с плавным сужением. Диаметр выходного сечения сопла 2,15 мм. Суживающийся участок сопла заканчивается коротким цилиндрическим участком с отверстием для отбора и регистрации давления в выходном сечении сопла Р2′. Измерительная диафрагма 1 представляет собой тонкий диск с круглым отверстием по центру (диаметр отверстия указан на стенде) и вместе с дифманометром 5 служит для измерения расхода воздуха. Температура воздуха перед измерительной диафрагмой замеряется с помощью термопары 6 в комплекте с потенциометром 7, а перед соплом – термопарой 8 в комплекте с потенциометром 9. Температура и давление воздуха в окружающей среде измеряются соответственно ртутным жидкостным термометром 10 и чашечным барометром 11. Порядок проведения опыта 1. Экспериментальное исследование процесса истечения заключается в измерении действительного расхода воздуха при различных давлениях в камере за соплом, т.е. при различных отношениях давлений β=Р2/Р1, начиная с β=1 и кон чая минимально возможным. 2. Проверить состояние всех измерительных приборов. Включить компрессор при полностью закрытом вентиле 4. После того как давление воздуха в ресивере достигнет требуемого значения, записать показания первого опыта в таблицу наблюдений 1. При этом перепад давлений в сопловом канале отсутствует, и расход воздуха равен 0. Все четыре манометра должны показывать одинаковые значения. 3. Далее следует плавно открыть вентиль 4, понизив давление за соплом до отношения β–0,95. После того как установится стационарный режим, характеризующийся постоянством давлений, снять показания приборов и записать их в протокол наблюдений (табл. 1). 4. Изменив расход воздуха с помощью вентиля 4 и понизив давление за соплом Р2 до значения β – 0,9, продолжить запись показаний приборов в протокол наблюдений. 5. Вблизи критического отношения давлений β ≈ 0,5 рекомендуется уменьшить шаг изменения β до 0,05. 5. Расчетные формулы и расчеты. 1. Атмосферное давление находится с учетом температурного расширения столбика ртути барометра по формуле:
2. Перевод показаний образцовых манометров Рм, Р1м, Р2м' и Р2м в абсолютные значения давлений определяем по формуле
где g – ускорение свободного падения, равное 9,81 м/с2; Рмj – показания одного из четырех манометров из табл. 1; Рв.п – верхний предел измерения давления соответствующего образцового манометра, кгс/см2. 3. Перепад давления воздуха на диафрагме
где ρ – плотность воды в U-образном вакуумметре, равная 1000 кг/м3; Н – показание дифманометра, переведенное в м вод.ст. 4. Плотность воздуха по состоянию перед диафрагмой
где R – характеристическая газовая постоянная воздуха, равная 287 Дж/кг·К. 5. Действительный расход воздуха через диафрагму (следовательно, через сопло)
6. Теоретическая скорость истечения в выходном сечении сопла
7. Значения энтальпий воздуха h1 и h2 в сечениях на входе и на выходе из сопла определяются по общему уравнению
где ср – теплоемкость воздуха при постоянном давлении, которая может быть принята не зависящей от температуры и равной 1,006 кДж/(кг·°С); tj – температура в рассматриваемом сечении, °С; j – индекс рассматриваемого сечения. 8. Теоретическое значение температуры в выходном сечении сопла находится из условия адиабатного процесса истечения по формуле
где β – значение отношения давлений. Величину β принимают по данным таблицы результатов расчета (табл. 2) для конкретного опыта, когда режим истечения докритический, т.е. β > βкр; для всех остальных опытов, когда β = βкр – критический и β < βкр– сверхкритический режимы, величина β в формуле (6) равна βкр (независимо от данных таблицы 2), и находится по уравнению(1) при k = 1,4. 9. Действительный процесс истечения сопровождается увеличением энтропии и температуры Т2д (рис. 2), которая может быть найдена при совместном решении двух уравнений:
Преобразование системы уравнений (7) относительно Т2д приводит к виду
– с + в· Т2д + а· Т2д2 = 0, (8) где R = 287, Дж/(кг·град); Ср = 1,006 кДж/(кг·град); fmin = 3,629·10-6, м2. Решение уравнения (8) можно представить в виде
10. Коэффициент потери энергии находится по формуле (2). 11. Коэффициент потери скорости находится по формуле (3). 12. Коэффициент полезного действия канала рассчитывается по формуле (4) или (5). 13. Результаты расчетов должны быть продублированы в форме сводной табл.2. 14. По результатам расчетов построить в соответствующем масштабе график зависимости расхода газа от отношения давления.
Таблица 1
Примечание. При выполнении замеров необходимо дополнительно записать: предел измерения давления всех образцовых манометров (Рвп=……кгс/см2); диаметр отверстия диафрагмы d0=……мм; диаметр сопла dmin=……мм. Таблица 2
6. Контрольные вопросы. 1. Сформулируйте цель лабораторной работы и поясните, как она достигается. 2. Назовите основные узлы экспериментальной установки и укажите их назначение. 3. Дайте определение процессов истечения и дросселирования. 4. Напишите уравнение первого закона термодинамики применительно к процессу истечения. 5. Напишите уравнение первого закона термодинамики применительно к процессу дросселирования. 6. Как изменяется скорость истечения через суживающееся сопло при изменении β от 1 до 0 (покажите качественное изменение на графике расхода)? 7. Чем объясняется проявление критического режима при истечении? 8. В чем различие теоретического и действительного процессов истечения? 9. Как изображаются теоретический и действительный процессы истечения в координатах s – h? 10. Почему отличаются теоретическая и действительная температуры воздуха на выходе из сопла при истечении? 11. На каком основании процесс дросселирования используется при измерении расхода воздуха? 12. Как может изменяться температура воздуха в процессе дросселирования? 13. От чего зависят величины коэффициентов: потери скорости φс, потери энергии ζс и полезного действия канала ηк? 14. Какие каналы называются соплами? 15. От каких параметров зависят расход и скорость газа при истечении через сопло? 16. Почему температуры воздуха перед диафрагмой и перед соплом равны? 17. Как изменяются энтальпия и энтропия потока газа при прохождении через диафрагму? 18. Как изменяются энтальпия и энтропия потока газа при прохождении через сопло? Работа 5. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ТЕПЛОИЗОЛЯЦИОННОГО МАТЕРИАЛА (метод цилиндрического слоя). Цели работы Освоение одного из методов определения коэффициента теплопроводности вещества (метод цилиндрического слоя) и закрепление знаний по теории теплопроводности. Основные положения Теплопроводность – молекулярный перенос теплоты в среде с неоднородным распределением температуры посредством теплового движения микрочастиц. Перенос теплоты теплопроводностью в чистом виде имеет место только в твердых телах с малым коэффициентом термического расширения и выражается эмпирическим законом Био-Фурье, согласно которому вектор удельного теплового потока прямо пропорционален градиенту температуры:
Знак «минус» в уравнении (1) показывает, что направление теплового потока противоположно направлению градиента температуры, а коэффициент пропорциональности λ характеризует способность тел проводить теплоту и называется коэффициентом теплопроводности. Количественно коэффициент теплопроводности λ – это тепловой поток (Вт), проходящий через единицу поверхности (м2) при единичном градиенте температур (Κ/м), и имеющий размерность Вт/(м·Κ). Коэффициент теплопроводности – физическая характеристика, зависящая от химического состава и физического строения вещества, его температуры, влажности и ряда других факторов. Коэффициент теплопроводности имеет максимальные значения для чистых металлов и минимальные для газов. Рассмотрим цилиндрическую стенку (трубку) длиной l с внутренним r1 и внешним r2 радиусами (рис. 1). Заданы температуры T1 внутренней и T2 наружной поверхностей стенки. Условием одномерности теплового потока будет условие l >>> r2, откуда следует дq/дl = 0. Дифференциальное уравнение теплопроводности в цилиндрических координатах при λ=const и отсутствии внутреннего источника теплоты (Qv=0) имеет вид (r – текущий радиус)
При заданных граничных условиях r = r1; T = T1; r = r2; T = T2. Получим
Согласно уравнению (2) температура цилиндрической стенки меняется по логарифмической зависимости (рис. 1).
Мощность теплового потока Q = q·F через цилиндрическую поверхность площадью F = 2π ·r·l (l – длина цилиндрической стенки) есть постоянная величина, равная
Формулу (3) можно записать, используя понятие термического сопротивления:
где Удельный тепловой поток на единицу длины стенки ql = Q/l:
Таким образом, предлагаемый экспериментальный метод определения коэффициента теплопроводности основан на измерении: · мощности теплового потока, проходящего через цилиндрический слой; · перепада температур между внутренней и наружной поверхностями слоя тепловой изоляции; · геометрических характеристик слоя тепловой изоляции. |



 , Па.
, Па. , Па,
, Па, , Па,
, Па, , кг/м3,
, кг/м3,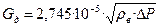 , кг/с.
, кг/с. , м/с.
, м/с. , кДж/кг,
, кДж/кг, , К,а t2 = T2 – 273, °C, (6)
, К,а t2 = T2 – 273, °C, (6)
 , м/с,
, м/с, , м/с.
, м/с. ;
;  ;
;  ;
; , К.
, К.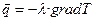 . (1)
. (1) .
. . (2)
. (2) Удельный тепловой поток q (поток через единицу площади цилиндрической поверхности) будет величиной переменной
Удельный тепловой поток q (поток через единицу площади цилиндрической поверхности) будет величиной переменной .
. . (3)
. (3) ,
, – термическое сопротивление цилиндрической стенки, м·Κ /Вт.
– термическое сопротивление цилиндрической стенки, м·Κ /Вт. .
.