ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Модуль нормального ускорения

12 3

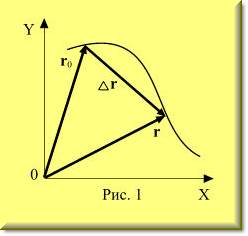
Кинематика. Основные формулы

Прежде всего, следует заметить, что речь будет идти о геометрической точке, то есть области пространства, не имеющей размеров. Именно для этого абстрактного образа (модели) и справедливы все представленные ниже определения и формулы. Однако для краткости я в дальнейшем буду часто говорить о движении тела,объектаили частицы. Это я делаю только для того, чтобы Вам легче было читать. Но всегда помните, что речь идет о геометрической точке.

Радиус-вектор точки - это вектор, начало которого совпадает с началом системы координат, а конец - с данной точкой. Радиус-вектор обозначается, как правило, буквой r.
Вектор перемещения (часто говорят просто – перемещение) – это вектор, начало которого совпадает с той точкой траектории, где было тело, когда мы начали изучать данное движение, а конец этого вектора совпадает с той точкой траектории, где мы это изучение закончили. Будем обозначать этот вектор как Δr. Использование символа Δ очевидно: Δr – это разность между радиус-вектором rконечной точки изучаемого отрезка траектории и радиус-вектором r₀ точки начала этого отрезка (рис. 1), то есть Δr =r − r₀.

Траектория - это линия, вдоль которой движется тело.

Путь - это сумма длин всех участков траектории, последовательно проходимых телом при движения. Обозначается либо ΔS, если речь идет об участке траектории, либо S, если речь идет о всей траектории наблюдаемого движения. Иногда (редко) путь обозначают и другой буквой, например, L (только не обозначайте его как r). Запомните! Путь - это положительный скаляр! Путь в процессе движения может только увеличиваться.

Средняя скорость перемещения v_ср - это вектор, определяемый выражением

v_ср = Δr/Δt.

Мгновенная скорость перемещения v- это вектор, определяемый выражением

v = dr/dt.

Средняя скорость путиv_ср - это скаляр, определяемый выражением

v_ср = Δs/Δt.

Часто встречаются и другие обозначения, например, <v>.

Мгновенная скорость пути v - это скаляр, определяемый выражением

v = ds/dt.

Модуль мгновенной скорости перемещения и мгновенная скорость пути - это одно и то же, поскольку dr = ds.

Среднее ускорениеa_ср - это вектор, определяемый выражением

a_ср = Δv/Δt.

Мгновенное ускорение(или просто, ускорение) a - это вектор, определяемый выражением

a =dv/dt.

Касательное (тангенциальное) ускорение a_τ (нижний индекс - это греческая строчная буква тау) - это вектор, являющийсявекторной проекцией мгновенного ускорения на касательную ось.

Нормальное (центростремительное) ускорение a_n - это вектор, являющийсявекторной проекцией мгновенного ускорения на ось нормали.

Модуль касательного ускорения

| a_τ | = dv/dt,

то есть это - производная модуля мгновенной скорости по времени.

Модуль нормального ускорения

| a_n | = v²/r,

где r - величина радиуса кривизны траектории в точке нахождения тела.

Важно! Хочу обратить внимание на следующее. Не путайтесь с обозначениями, касающимися касательного и нормального ускорений! Дело в том, что в литературе по этому поводу традиционно наблюдается полная чехарда.

Запомните!

a_τ - это вектор касательного ускорения,

a_n - это вектор нормального ускорения.

a_τ и a_n являются векторными проекциями полного ускорения а на касательную ось и ось нормали соответственно,

a_τ - это проекция (скалярная!) касательного ускорения на касательную ось,

a_n - это проекция (скалярная!) нормального ускорения на ось нормали,

| a_τ |- это модульвектора касательного ускорения,

| a_n | - это модульвектора нормального ускорения.

Не зная азов векторной алгебры или пренебрегая ими, очень легко полностью запутаться при изучении и анализе физических процессов. Поэтому знание векторной алгебры является наиглавнейшим условием успеха в изучении механики. И не только механики. В дальнейшем, при изучении других разделов физики, Вы неоднократно в этом убедитесь.

Мгновенная угловая скорость(или просто, угловая скорость) ω- это вектор, определяемый выражением

ω = dφ/dt,

где dφ- бесконечно малое изменение угловой координаты (dφ- вектор!).

Мгновенное угловое ускорение(или просто, угловое ускорение) ε- это вектор, определяемый выражением

ε= dω/dt.

Связь между v, ω и r:

v =ω ×r.

Связь между v, ω и r:

v = ω · r.

Связь между | a_τ |, ε и r:

| a_τ | = ε · r.

Теперь перейдем ккинематическим уравнениям конкретных видов движения. Эти уравнения надо выучить наизусть.

Кинематическое уравнение равномерного и прямолинейного движенияимеет вид:

r = r₀ + v t,

гдеr- радиус-вектор объекта в момент времени t, r₀ - то же в начальный момент времени t₀ (в момент начала наблюдений).

Кинематическое уравнение движения с постоянным ускорениемимеет вид:

r = r₀ + v₀ t + at²/2, где v₀ скорость объекта в момент t₀ .

Уравнение для скорости тела при движении с постоянным ускорениемимеет вид:

v= v₀ + a t.

Кинематическое уравнение равномерного движения по окружности в полярных координатахимеет вид:

φ = φ₀ + ω_z t,

где φ - угловая координата тела в данный момент времени, φ₀ - угловая координата тела в момент начала наблюдения (в начальный момент времени), ω_z - проекция угловой скорости ωна ось Z (обычно эта ось выбирается перпендикулярно плоскости вращения).

12 3