ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Тема 2. Движение с постоянной скоростью.

123

Номер варианта	Номер задачи	Номер задачи

Задача 1. Тело движется равномерно и прямолинейно от пункта А к пункту В со скоростью, величина которой v = 70 км/ч. Найти расстояния L₁ и L₂, на которых будет находиться тело относительно пункта В через t₁ = 0,3 ч и t₂ = 1,3 ч соответственно, считая, что в пункте А оно находилось в момент t = t₀ = 0. Расстояние между пунктами L = 10 км. Найти пути S₁ и S₂, которые были пройдены за t₁ и t₂ соответственно.

Задача2. По прямолинейному шоссе движутся равномерно в противоположных направлениях автобус и мотоциклист. В момент начала наблюдения координаты автобуса и мотоциклиста и модули их скоростей соответственно равны: x_0a = 120 м, x_0м = − 340 м, v_а = 30 м/с, v_м = 20 м/с (см. рисунок). Написать уравнения движения автобуса и мотоциклиста. Найти положения этих объектов через t₁ = 10 c после начала наблюдения. В какой момент времени положение каждого из них совпадало с началом системы координат? Когда и где произошла их встреча? Каким будет расстояние L₂ между ними через t₂ = 2 мин после начала наблюдения? Построить графики зависимости от времени координат автобуса и мотоциклиста и расстояния между ними.

Задача3. Тело движется равномерно по прямолинейному шоссе со скоростью, величина которой v = 10 м/с и последовательно проходит через пункты А, В и С. Расстояние между А и В равно АВ = 90 км, расстояние между В и С равно ВС = 10 км. Сколько времени понадобится телу, чтобы пройти расстояния между А и В, А и С, В и С? Где будет находиться тело спустя 1,5 часа, после прохождения пункта А? Как будет изменяться со временем расстояние между телом и пунктом С? Построить график зависимости изменения этого расстояния от времени. Где и на каком расстоянии от пункта А находилось тело за 20 минут до того момента, как оно поравнялось с этим пунктом?

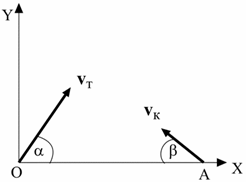
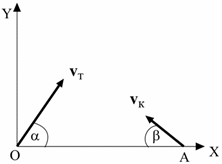
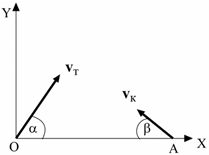
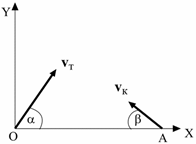
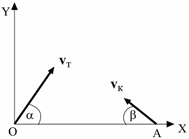
Задача4. Торпеду выпускают из точки О, когда корабль противника находится в точке А, двигаясь со скоростью, величина которой v_к = 70 км/ч и направленной под углом β = 35 градусов к линии ОА (см. рисунок). Величина скорости торпеды v_т = 120 км/ч. Под каким углом α ее надо выпустить, чтобы она поразила цель? Каково время t₁ движения торпеды от момента ее выпуска до поражения цели? Расстояние между точками О и А 1000 метров.

Задача5. По прямолинейному участку шоссе движется автомобиль со скоростью, равной по величине v_a = 40 км/ч. Пешеход находится на расстоянии b = 30 м от шоссе и a = 600 м от автомобиля. С какой минимальной по величине скоростью v_п _min он должен двигаться, чтобы встретить автомобиль, и сколько времени t₁ он на это затратит? В каком направлении (по отношению к первоначальному направлению на автомобиль) пешеход при этом должен двигаться?

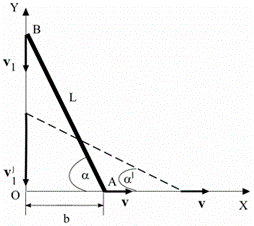
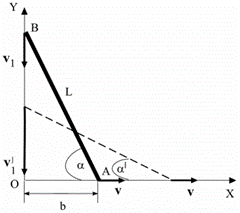
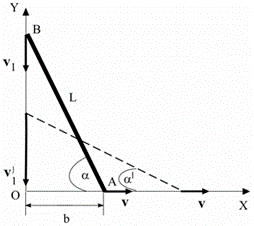
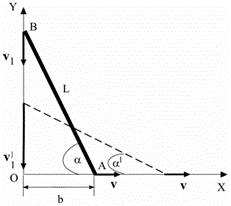
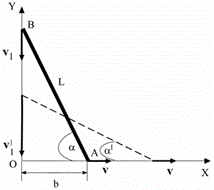
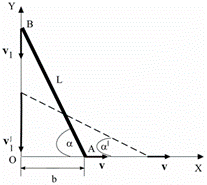
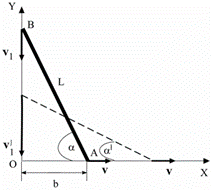
Задача6. Стержень АВ длиной L = 2 м опирается концами о пол и стену. Найти зависимость ординаты конца В от времени при движении конца А вдоль оси X с постоянной скоростью, равной по величине v = 0,5 м/с, от положения, указанного на рисунке (b = 0,8 м). Будет ли равномерным движение конца В? Найти величину скорости v'₁ конца В, когда угол α' = 40⁰ (см. рисунок).

Задача7. На наклонную плоскость, составляющую с горизонтом угол α, опирается стержень, который может перемещаться только по вертикали благодаря направляющему устройству. С какой по величине скоростью v_ст поднимается стержень, если наклонная плоскость движется с постоянной скоростью, величина которой равна v = 10 м/с?

Задача8. Автомобиль, двигаясь со скоростью, величина которой v₁ = 40 км/ч, проехал половину пути до места назначения за некоторый промежуток времени t₁. С какой по величине скоростью v₂ он должен продолжать движение, чтобы за такое же время достигнуть цели и вернуться обратно?

Задача 9. Тело движется равномерно и прямолинейно от пункта А к пункту В со скоростью, величина которой v = 65 км/ч. Найти расстояния L₁ и L₂, на которых будет находиться тело относительно пункта В через t₁ = 0,5 ч и t₂ = 3 ч соответственно, считая, что в пункте А оно находилось в момент t = t₀ = 0. Расстояние между пунктами L = 30 км. Найти пути S₁ и S₂, которые были пройдены за t₁ и t₂ соответственно.

Задача10. По прямолинейному шоссе движутся равномерно в противоположных направлениях автобус и мотоциклист. В момент начала наблюдения координаты автобуса и мотоциклиста и модули их скоростей соответственно равны: x_0a = 140 м, x_0м = − 360 м, v_а = 30 м/с, v_м = 15 м/с (см. рисунок). Написать уравнения движения автобуса и мотоциклиста. Найти положения этих объектов через t₁ = 15 c после начала наблюдения. В какой момент времени положение каждого из них совпадало с началом системы координат? Когда и где произошла их встреча? Каким будет расстояние L₂ между ними через t₂ = 2,5 мин после начала наблюдения? Построить графики зависимости от времени координат автобуса и мотоциклиста и расстояния между ними.

Задача11. Тело движется равномерно по прямолинейному шоссе со скоростью, величина которой v = 8 м/с и последовательно проходит через пункты А, В и С. Расстояние между А и В равно АВ = 60 км, расстояние между В и С равно ВС = 30 км. Сколько времени понадобится телу, чтобы пройти расстояния между А и В, А и С, В и С? Где будет находиться тело спустя 2 час, после прохождения пункта А? Как будет изменяться со временем расстояние между телом и пунктом С? Построить график зависимости изменения этого расстояния от времени. Где и на каком расстоянии от пункта А находилось тело за 25 минут до того момента, как оно поравнялось с этим пунктом?

Задача12. Торпеду выпускают из точки О, когда корабль противника находится в точке А, двигаясь со скоростью, величина которой v_к = 50 км/ч и направленной под углом β = 30 градусов к линии ОА (см. рисунок). Величина скорости торпеды v_т = 100 км/ч. Под каким углом α ее надо выпустить, чтобы она поразила цель? Каково время t₁ движения торпеды от момента ее выпуска до поражения цели? Расстояние между точками О и А 500 метров.

Задача13. По прямолинейному участку шоссе движется автомобиль со скоростью, равной по величине v_a = 70 км/ч. Пешеход находится на расстоянии b = 88 м от шоссе и a = 670 м от автомобиля. С какой минимальной по величине скоростью v_п _min он должен двигаться, чтобы встретить автомобиль, и сколько времени t₁ он на это затратит? В каком направлении (по отношению к первоначальному направлению на автомобиль) пешеход при этом должен двигаться?

Задача14. Стержень АВ длиной L = 0.8 м опирается концами о пол и стену. Найти зависимость ординаты конца В от времени при движении конца А вдоль оси X с постоянной скоростью, равной по величине v = 0,1 м/с, от положения, указанного на рисунке (b = 0,5 м). Будет ли равномерным движение конца В? Найти величину скорости v'₁ конца В, когда угол α' = 60⁰ (см. рисунок).

Задача15. На наклонную плоскость, составляющую с горизонтом угол α, опирается стержень, который может перемещаться только по вертикали благодаря направляющему устройству. С какой по величине скоростью v_ст поднимается стержень, если наклонная плоскость движется с постоянной скоростью, величина которой равна v = 15 м/с?

Задача16. Автомобиль, двигаясь со скоростью, величина которой v₁ = 26 км/ч, проехал половину пути до места назначения за некоторый промежуток времени t₁. С какой по величине скоростью v₂ он должен продолжать движение, чтобы за такое же время достигнуть цели и вернуться обратно?

Задача 17. Тело движется равномерно и прямолинейно от пункта А к пункту В со скоростью, величина которой v = 80 км/ч. Найти расстояния L₁ и L₂, на которых будет находиться тело относительно пункта В через t₁ = 1 ч и t₂ = 2,5 ч соответственно, считая, что в пункте А оно находилось в момент t = t₀ = 0. Расстояние между пунктами L = 50 км. Найти пути S₁ и S₂, которые были пройдены за t₁ и t₂ соответственно.

Задача18. По прямолинейному шоссе движутся равномерно в противоположных направлениях автобус и мотоциклист. В момент начала наблюдения координаты автобуса и мотоциклиста и модули их скоростей соответственно равны: x_0a = 90 м, x_0м = − 300 м, v_а = 18 м/с, v_м = 15 м/с (см. рисунок). Написать уравнения движения автобуса и мотоциклиста. Найти положения этих объектов через t₁ = 5 c после начала наблюдения. В какой момент времени положение каждого из них совпадало с началом системы координат? Когда и где произошла их встреча? Каким будет расстояние L₂ между ними через t₂ = 3,5 мин после начала наблюдения? Построить графики зависимости от времени координат автобуса и мотоциклиста и расстояния между ними.

Задача19. Тело движется равномерно по прямолинейному шоссе со скоростью, величина которой v = 3 м/с и последовательно проходит через пункты А, В и С. Расстояние между А и В равно АВ = 75 км, расстояние между В и С равно ВС = 17 км. Сколько времени понадобится телу, чтобы пройти расстояния между А и В, А и С, В и С? Где будет находиться тело спустя 0,5 часа, после прохождения пункта А? Как будет изменяться со временем расстояние между телом и пунктом С? Построить график зависимости изменения этого расстояния от времени. Где и на каком расстоянии от пункта А находилось тело за 5 минут до того момента, как оно поравнялось с этим пунктом?

Задача20. Торпеду выпускают из точки О, когда корабль противника находится в точке А, двигаясь со скоростью, величина которой v_к = 40 км/ч и направленной под углом β = 20 градусов к линии ОА (см. рисунок). Величина скорости торпеды v_т = 150 км/ч. Под каким углом α ее надо выпустить, чтобы она поразила цель? Каково время t₁ движения торпеды от момента ее выпуска до поражения цели? Расстояние между точками О и А 300 метров.

Задача21. По прямолинейному участку шоссе движется автомобиль со скоростью, равной по величине v_a = 34 км/ч. Пешеход находится на расстоянии b = 100 м от шоссе и a = 350 м от автомобиля. С какой минимальной по величине скоростью v_п _min он должен двигаться, чтобы встретить автомобиль, и сколько времени t₁ он на это затратит? В каком направлении (по отношению к первоначальному направлению на автомобиль) пешеход при этом должен двигаться?

Задача22. Стержень АВ длиной L = 3 м опирается концами о пол и стену. Найти зависимость ординаты конца В от времени при движении конца А вдоль оси X с постоянной скоростью, равной по величине v = 0,8 м/с, от положения, указанного на рисунке (b = 1,2 м). Будет ли равномерным движение конца В? Найти величину скорости v'₁ конца В, когда угол α' = 35⁰ (см. рисунок).

Задача23. На наклонную плоскость, составляющую с горизонтом угол α, опирается стержень, который может перемещаться только по вертикали благодаря направляющему устройству. С какой по величине скоростью v_ст поднимается стержень, если наклонная плоскость движется с постоянной скоростью, величина которой равна v?

Задача24. Автомобиль, двигаясь со скоростью, величина которой v₁ = 72 км/ч, проехал половину пути до места назначения за некоторый промежуток времени t₁. С какой по величине скоростью v₂ он должен продолжать движение, чтобы за такое же время достигнуть цели и вернуться обратно?

Задача 25. Тело движется равномерно и прямолинейно от пункта А к пункту В со скоростью, величина которой v = 50 км/ч. Найти расстояния L₁ и L₂, на которых будет находиться тело относительно пункта В через t₁ = 1,5 ч и t₂ = 3,5 ч соответственно, считая, что в пункте А оно находилось в момент t = t₀ = 0. Расстояние между пунктами L = 80 км. Найти пути S₁ и S₂, которые были пройдены за t₁ и t₂ соответственно.

Задача26. По прямолинейному шоссе движутся равномерно в противоположных направлениях автобус и мотоциклист. В момент начала наблюдения координаты автобуса и мотоциклиста и модули их скоростей соответственно равны: x_0a = 80 м, x_0м = − 400 м, v_а = 25 м/с, v_м = 20 м/с (см. рисунок). Написать уравнения движения автобуса и мотоциклиста. Найти положения этих объектов через t₁ = 10 c после начала наблюдения. В какой момент времени положение каждого из них совпадало с началом системы координат? Когда и где произошла их встреча? Каким будет расстояние L₂ между ними через t₂ = 0,5 мин после начала наблюдения? Построить графики зависимости от времени координат автобуса и мотоциклиста и расстояния между ними.

Задача27. Тело движется равномерно по прямолинейному шоссе со скоростью, величина которой v = 9 м/с и последовательно проходит через пункты А, В и С. Расстояние между А и В равно АВ = 95 км, расстояние между В и С равно ВС = 50 км. Сколько времени понадобится телу, чтобы пройти расстояния между А и В, А и С, В и С? Где будет находиться тело спустя 2,5 часа, после прохождения пункта А? Как будет изменяться со временем расстояние между телом и пунктом С? Построить график зависимости изменения этого расстояния от времени. Где и на каком расстоянии от пункта А находилось тело за 30 минут до того момента, как оно поравнялось с этим пунктом?

Задача28. Торпеду выпускают из точки О, когда корабль противника находится в точке А, двигаясь со скоростью, величина которой v_к = 70 км/ч и направленной под углом β = 40 градусов к линии ОА (см. рисунок). Величина скорости торпеды v_т = 170 км/ч. Под каким углом α ее надо выпустить, чтобы она поразила цель? Каково время t₁ движения торпеды от момента ее выпуска до поражения цели? Расстояние между точками О и А 730 метров.

Задача29. По прямолинейному участку шоссе движется автомобиль со скоростью, равной по величине v_a = 44 км/ч. Пешеход находится на расстоянии b = 90 м от шоссе и a = 200 м от автомобиля. С какой минимальной по величине скоростью v_п _min он должен двигаться, чтобы встретить автомобиль, и сколько времени t₁ он на это затратит? В каком направлении (по отношению к первоначальному направлению на автомобиль) пешеход при этом должен двигаться?

Задача30. Стержень АВ длиной L = 2,3 м опирается концами о пол и стену. Найти зависимость ординаты конца В от времени при движении конца А вдоль оси X с постоянной скоростью, равной по величине v = 0,9 м/с, от положения, указанного на рисунке (b = 0,3 м). Будет ли равномерным движение конца В? Найти величину скорости v'₁ конца В, когда угол α' = 55⁰ (см. рисунок).

Задача31. На наклонную плоскость, составляющую с горизонтом угол α, опирается стержень, который может перемещаться только по вертикали благодаря направляющему устройству. С какой по величине скоростью v_ст поднимается стержень, если наклонная плоскость движется с постоянной скоростью, величина которой равна v = 19 м/с?

Задача32. Автомобиль, двигаясь со скоростью, величина которой v₁ = 90 км/ч, проехал половину пути до места назначения за некоторый промежуток времени t₁. С какой по величине скоростью v₂ он должен продолжать движение, чтобы за такое же время достигнуть цели и вернуться обратно?

Задача33. Стержень АВ длиной L = 2 м опирается концами о пол и стену. Найти зависимость ординаты конца В от времени при движении конца А вдоль оси X с постоянной скоростью, равной по величине v = 0,1 м/с, от положения, указанного на рисунке (b = 1 м). Будет ли равномерным движение конца В? Найти величину скорости v'₁ конца В, когда угол α' = 35⁰ (см. рисунок).

Задача34. На наклонную плоскость, составляющую с горизонтом угол α, опирается стержень, который может перемещаться только по вертикали благодаря направляющему устройству. С какой по величине скоростью v_ст поднимается стержень, если наклонная плоскость движется с постоянной скоростью, величина которой равна v = 20 м/с?

Задача35. Стержень АВ длиной L = 4 м опирается концами о пол и стену. Найти зависимость ординаты конца В от времени при движении конца А вдоль оси X с постоянной скоростью, равной по величине v = 1 м/с, от положения, указанного на рисунке (b = 3,6 м). Будет ли равномерным движение конца В? Найти величину скорости v'₁ конца В, когда угол α' = 40⁰ (см. рисунок).

Задача 36. Тело движется равномерно и прямолинейно от пункта А к пункту В со скоростью, величина которой v = 36 км/ч. Найти расстояния L₁ и L₂, на которых будет находиться тело относительно пункта В через t₁ = 0,2 ч и t₂ = 0,5 ч соответственно, считая, что в пункте А оно находилось в момент t = t₀ = 0. Расстояние между пунктами L = 10 км. Найти пути S₁ и S₂, которые были пройдены за t₁ и t₂ соответственно.

Задача37. По прямолинейному шоссе движутся равномерно в противоположных направлениях автобус и мотоциклист. В момент начала наблюдения координаты автобуса и мотоциклиста и модули их скоростей соответственно равны: x_0a = 60 м, x_0м = − 200 м, v_а = 10 м/с, v_м = 5 м/с (см. рисунок). Написать уравнения движения автобуса и мотоциклиста. Найти положения этих объектов через t₁ = 10 c после начала наблюдения. В какой момент времени положение каждого из них совпадало с началом системы координат? Когда и где произошла их встреча? Каким будет расстояние L₂ между ними через t₂ = 0,5 мин после начала наблюдения? Построить графики зависимости от времени координат автобуса и мотоциклиста и расстояния между ними.

Задача38. Тело движется равномерно по прямолинейному шоссе со скоростью, величина которой v = 15 м/с и последовательно проходит через пункты А, В и С. Расстояние между А и В равно АВ = 100 км, расстояние между В и С равно ВС = 15 км. Сколько времени понадобится телу, чтобы пройти расстояния между А и В, А и С, В и С? Где будет находиться тело спустя 1 час, после прохождения пункта А? Как будет изменяться со временем расстояние между телом и пунктом С? Построить график зависимости изменения этого расстояния от времени. Где и на каком расстоянии от пункта А находилось тело за 25 минут до того момента, как оно поравнялось с этим пунктом?

Задача39. Торпеду выпускают из точки О, когда корабль противника находится в точке А, двигаясь со скоростью, величина которой v_к = 36 км/ч и направленной под углом β = 45 градусов к линии ОА (см. рисунок). Величина скорости торпеды v_т = 50 км/ч. Под каким углом α ее надо выпустить, чтобы она поразила цель? Каково время t₁ движения торпеды от момента ее выпуска до поражения цели? Расстояние между точками О и А 350 метров.

Задача40. По прямолинейному участку шоссе движется автомобиль со скоростью, равной по величине v_a = 60 км/ч. Пешеход находится на расстоянии b = 70 м от шоссе и a = 600 м от автомобиля. С какой минимальной по величине скоростью v_п _min он должен двигаться, чтобы встретить автомобиль, и сколько времени t₁ он на это затратит? В каком направлении (по отношению к первоначальному направлению на автомобиль) пешеход при этом должен двигаться?

Задача41. Стержень АВ длиной L = 2,2 м опирается концами о пол и стену. Найти зависимость ординаты конца В от времени при движении конца А вдоль оси X с постоянной скоростью, равной по величине v = 0,7 м/с, от положения, указанного на рисунке (b = 0,9 м). Будет ли равномерным движение конца В? Найти величину скорости v'₁ конца В, когда угол α' = 30⁰ (см. рисунок).

Задача42. На наклонную плоскость, составляющую с горизонтом угол α, опирается стержень, который может перемещаться только по вертикали благодаря направляющему устройству. С какой по величине скоростью v_ст поднимается стержень, если наклонная плоскость движется с постоянной скоростью, величина которой равна v = 6 м/с?

Задача43. Автомобиль, двигаясь со скоростью, величина которой v₁ = 16 км/ч, проехал половину пути до места назначения за некоторый промежуток времени t₁. С какой по величине скоростью v₂ он должен продолжать движение, чтобы за такое же время достигнуть цели и вернуться обратно?

123