 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Примеры решения задач по машинам постоянного тока
Министерство сельского хозяйства и продовольствия Республики Беларусь Учреждение образования Технический университет»
В помощь абитуриенту
ЭЛЕКТРИЧЕСКИЕ МАШИНЫ
Специальность – Энергетическое обеспечение сельского хозяйства
Минск МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
УТВЕРЖДАЮ Ректор БГАТУ _______________Н.В. Казаровец «____»_________________2007г.
Перечень основных тем, образцы типовых задач И экзаменационного задания Для подготовки к вступительному экзамену По дисциплине «Электрические машины и аппараты» (для абитуриентов, окончивших аграрные колледжи)
Минск УДК 321.313(07) ББК 31.261я7 Э 45
Рекомендовано научно-методическим советом Учреждения образования «Белорусский государственный аграрный технический университет» (протокол №1 от 22.02.2007г.)
Составитель – Н.Е. Шевчик
В пособии изложены основные темы для подготовки к вступительному экзамену по дисциплине «Электрические машины и аппараты» для слушателей подготовительных курсов при агротехнических колледжах, даны типовые задачи и образец экзаменационного задания. Предназначено для абитуриентов Учреждения образования «Белорусский государственный университет», окончивших аграрные колледжи.
УДК 321.313(07) ББК 31.261я7
© БГАТУ, 2007
Введение
Экзаменационное задание для вступительного испытания по дисциплине «Электрические машины и аппараты» состоит из задач различной степени сложности. С порядковым номером задачи сложность возрастает. При проверке на ЭВМ проверяется цифра ответа. Если она не точна, задача считается не решенной, т.е. оценивается не только правильность решения, но и точность алгебраических преобразований и арифметических расчетов. Экзаменационные задачи составлены по четырем разделам: машины постоянного тока, асинхронные машины, синхронные машины и трансформаторы. Учебно-тематический план для слушателей подготовительных курсов составлен таким образом, чтобы максимально ориентировать учащихся на решение задач, и его назначение — дополнить основной курс «Электрические машины и аппараты». В теоретической части приведена информация, на которую необходимо обратить внимание при подготовке к вступительным экзаменам. Она используется при решении задач в первую очередь. Но это не означает, что ее достаточно для подготовки к экзамену. Примеры решения задач максимально приближены к тем, которые будут на вступительных экзаменах; в них указана размерность ответа. В примере экзаменационного задания приведены задачи вступительного испытания по дисциплине «Электрические машины и аппараты» 2006 года.
ОСНОВНЫЕ ТЕМЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
Машины постоянного тока
ЭДС машины постоянного тока:
где Е — ЭДС машины постоянного тока, В; Ф — основной магнитный поток, Вб;
где
В простой петлевой обмотке Момент машины постоянного тока:
где М — момент машины постоянного тока, Н×м;
Соотношение между постоянными момента и ЭДС:
Уравнения равновесия напряжений: — для генератора:
где
— для двигателя:
Частота вращения двигателя постоянного тока: — с параллельным возбуждением:
— с последовательным возбуждением:
где к — коэффициент пропорциональности меду током и магнитным потоком в двигателе последовательного возбуждения.
Формула, связывающая момент, мощность на валу и частоту вращения якоря:
При расчете по формуле (1.10) необходимо соблюдать размерности: момента (Н×м), мощности (кВт), частоты вращения (мин-1). Потери, коэффициент полезного действия, подводимая или присоединенная мощность иллюстрируются энергетической диаграммой (рисунок 1.1)
На диаграмме: Р1 — подводимая или присоединенная мощность, Вт, двигатель потребляет ее из сети; U — напряжение сети, В; I — ток двигателя, А; Рэм — электромагнитная мощность двигателя, Вт; из рисунка видно: Рэм =Р1 - DРэл, (1.11)
где DРэл — электрические потери двигателя, Вт;
где
где DРм — магнитные потери, Вт; DРмех — механические потери, Вт; DРдоб — добавочные потери, Вт.
Коэффициент полезного действия двигателя
Двигатель потребляет электрическую мощность из сети, преобразует ее в механическую и через вал передает ее на рабочую машину. Часть мощности теряется в двигателе, что учитывается коэффициентом полезного действия. У генератора наоборот: механическая мощность поступает через вал приводного двигателя (турбины), преобразуется в электрическую и поступает в электрическую сеть. Примеры решения задач по машинам постоянного тока Задача 1 Определить электромагнитную мощность двигателя постоянного тока (кВт), если ток якоря Iя = 10 А, число проводников обмотки якоря N = 180 шт., магнитный поток Ф = 0,07 Вб, частота вращения n = 1500 мин-1. Обмотка якоря простая петлевая, ширина щетки равна ширине коллекторной пластины. {Ответ с точностью до двух знаков после запятой.} Решение Электромагнитная мощность двигателя (кВт):
Электромагнитный момент машины постоянного тока (Н×м):
Постоянная машины при расчете момента
Ширина щетки равна ширине коллекторной пластины, обмотка простая петлевая, поэтому количество пар параллельных ветвей равно количеству пар полюсов: а = р, — тогда
С учетом вышеизложенного
Ответ: Рэм = 3,15 кВт. Задача 2 Четырехполюсная машина постоянного тока независимого возбуждения имеет следующие параметры: диаметр якоря D = 0,2 м, длина якоря l = 0,4 м, число проводников обмотки якоря N = 540, индукция в воздушном зазоре B = 0,4 Тл, обмотка якоря простая петлевая, ширина щетки равна ширине коллекторной пластины. Частота вращения машины, работающей в режиме генератора, n = 1000 мин-1, напряжение на нагрузке Uг = 220 В. Определить частоту вращения при работе этой же машины в режиме двигателя, если токи возбуждения и якоря остались неизменными, двигатель питается от сети Uд = 220 В. В расчете индукцию в воздушном зазоре считать постоянной по всей длине зазора, падением напряжения на щетках пренебречь {ответ с точностью до целого числа}. Решение Частота вращения двигателя (падением напряжения на щетках пренебречь)
Сопротивление обмотки якоря определится из формулы равновесия ЭДС генератора:
Подставляем полученное выражение расчета сопротивления обмотки якоря в формулу частоты вращения двигателя:
Постоянная машины при определении ЭДС
Количество пар полюсов — р = 2 (из условия). Ширина щетки равна ширине коллекторной пластины, обмотка простая петлевая, поэтому количество пар параллельных ветвей равно количеству пар полюсов: а = р, — тогда
Так как принято допущение, что индукция в воздушном зазоре постоянная по всей длине зазора, магнитный поток можно рассчитать по формуле:
Частота вращения двигателя
Ответ: nд = 945 мин-1.
Задача 3 Двигатель постоянного тока подключен к сети напряжением U = 440 В. Требуется рассчитать его магнитный поток (Вб), если его мощность на валу Р2 = 10 кВт, сопротивление обмотки якоря rя = 0,07 Ом, число проводников обмотки якоря N = 240, частота вращения n = 1000 мин-1. Реакцией якоря и падением напряжения на щетках пренебречь, обмотка якоря простая петлевая, одноходовая. {Ответ с точностью до трех знаков после запятой.} Решение Из уравнений:
Полученное выражение подставим в формулу:
Сделав алгебраические преобразования, получим квадратное уравнение:
Для простой петлевой, одноходовой обмотки якоря а = р, поэтому
Подставляем числовые значения в систему уравнений:
Дискриминант системы D = 278423´109. Корни уравнения: Ф1 = 0; Ф2 = 0,1096 Вб. Ответ: Ф = 0,110 Вб. ОБЩИЕ ВОПРОСЫ МАШИН ПЕРЕМЕННОГО ТОКА. СИНХРОННЫЕ МАШИНЫ
В основе действия любой машины переменного тока лежит вращающееся магнитное поле. Для получения указанного поля при трёхфазной системе должны выполняться два условия: 1. Обмотки фаз должны быть сдвинуты друг относительно друга на 120 электрических градусов (число электрических градусов в машине зависит от числа пар полюсов: на одну пару полюсов приходится 360 электрических градусов); 2. Токи в фазах должны быть сдвинуты во времени друг от друга на 1/3 периода. Обмотка машины переменного тока строится по обмоточным данным: · шаг обмотки
где
Р — число пар полюсов, шт.;
· число пазов на полюс и фазу
где
· число катушечных групп. Для однослойной обмотки
В двухслойной обмотке:
· число электрических градусов на один паз:
· параллельные ветви. Если катушечные группы одной фазы соединены последовательно, тогда число параллельных ветвей Число пар полюсов в машине переменного тока
где f — частота тока, Гц; n1 — частота вращения магнитного поля статора, мин-1. Электродвижущая сила одной фазы обмотки машины переменного тока:
где Ф — магнитный поток, Вб; W — число витков обмотки, шт.; Коб — обмоточный коэффициент;
где Ку — коэффициент укорочения; Кр — коэффициент распределения; Кс — коэффициент скоса;
где
Электромагнитная мощность синхронной машины, подключенной к сети:
где Е0 — ЭДС, наводимая основным магнитным потоком, В; рассчитывается по формуле (2.7); U1ф — фазное напряжение сети, В; xd, xq — индуктивное сопротивление реакции якоря по продольной и поперечной осям, Ом; для машины с неявнополюсным якорем xd =xq; q — нагрузочный угол, град. Уравнение равновесия напряжений синхронного генератора:
где
где
Упрощенная векторная диаграмма явнополюсного синхронного генератора, работающего на активно-индуктивную нагрузку, приведена на рисунке 2.1. При ее построении сделано допущение, что r1 = 0, и потоки рассеяния также равны нулю. Тогда получается прямоугольный треугольник с катетами Е1q и (E0-Е1d) а также гипотенузой U1. Облегчается решение задач.
Примеры решения задач по общим вопросам машин переменного тока Задача 1 В статоре с числом пазов Z = 36 уложена трехфазная обмотка, создающая вращающееся магнитное поле с частотой n = 1500 мин-1. Шаг обмотки укорочен на один паз. Частота тока в обмотке f = 50 Гц. Определить обмоточный коэффициент {ответ с точностью до трех знаков после запятой}. Решение Обмоточный коэффициент Коб = Ку ´ Кр ´ Кс. Коэффициент укорочения Ку = sin(Yу´90о/ Y), где Y и Yу — соответственно диаметральный и укороченный шаги обмотки; Y = Z/2P. Количество полюсов Р = 60f/n. Коэффициент распределения
Число пазов на полюс и фазу q = Z/2Pm. Число электрических градусов, приходящихся на один паз, a = 360Р/Z. Скоса пазов нет, поэтому Кс=1. Производим расчет: Р = 60 ´ 50/1500 = 2 ; Y = 36/(2 ´ 2) = 9; Yу = Y – 1 = 9 – 1 = 8; Ку = sin (8 ´ 90о/9) = 0,9848; q = 36/(2 ´ 2 ´ 3)=3; a = 360 ´ 2/36 = 20 эл. град ; Коб=0,9848´0,9598=0,9452. Ответ: Коб = 0,945.
Задача 2 Трехфазный явнополюсный синхронный генератор работает параллельно на сеть большой мощности. ЭДС фазы генератора Еоф = 254 В, напряжение сети U1 = 380 В, индуктивные сопротивления: по продольной оси хd = 0,19 Ом, по поперечной оси хq = 0,121 Ом; угол сдвига между напряжением и ЭДС (нагрузочный угол) θ = 30о, тормозной момент, создаваемый генератором М = 2155 Н×м, частота вращения n1 = 3000 мин-1, потери в обмотках статора DР1 = 3,4 кВт. Схема соединений обмоток статора — «звезда». Определить КПД генератора (%) {ответ с точностью до целого числа}. Решение КПД генератора определится по формуле: где Р1 — мощность, передаваемая на вал генератора от приводного двигателя, Р2 — полезная мощность генератора, если пренебречь потерями в обмотке статора, она равна электромагнитной:
В условии указано: «Напряжение сети U1 = 380 В». Это линейное напряжение, при соединении «звезда»
Ответ: h = 93%. АСИНХРОННЫЕ МАШИНЫ
Мощность на валу трехфазного асинхронного двигателя
где
cosφ1 — коэффициент мощности;
Частота вращения ротора
где
где Р — число пар полюсов;
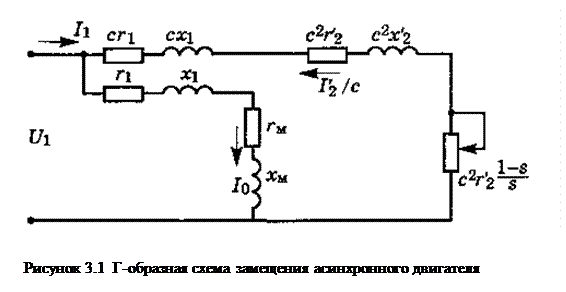
Схема замещения (Г-образная) асинхронного двигателя приведена на рисунке 3.1.
На рисунке 3.1 U1ф — фазное напряжение, В; С — коэффициент, примем С = 1; r1, x1 — сопротивления обмотки статора, Ом; r'2, x'2 — приведенные сопротивления обмотки ротора, Ом; rм, xм — сопротивления намагничивающей ветви, Ом; I1 — ток статора, А; I0 — намагничивающий ток, А; I'2 — приведенный ток ротора, А. Параметры схем определятся из опытов короткого замыкания и холостого хода по следующим формулам:
где rк — активное сопротивление короткого замыкания, Ом; Рк — потери короткого замыкания, Вт m — количество фаз; Iн — номинальный ток двигателя, А; zк — полное сопротивление короткого замыкания, Ом; Uкф — фазное напряжение короткого замыкания, В. Приведенные сопротивления обмотки ротора приблизительно равны сопротивлениям обмотки статора:
Параметры намагничивающей ветви:
где Рх — потери холостого хода, Вт; Iх — холостой ток двигателя, А; Zм — полное сопротивление намагничивающей ветви, Ом; Uхф — фазное напряжение холостого хода, В.
Мощность на валу двигателя Р2 будет соответствовать тепловым потерям на переменном сопротивлении r'2(1–s)/s:
Приведенный ток ротора I'2 также определяется по схеме замещения (рисунок 3.1):
где Рх — потери холостого хода, Вт.
При подстановке выражения (3.8) в формулу (3.7) получим уравнение мощности на валу:
Из формулы (3.9) видно, что мощность асинхронного двигателя пропорциональна квадрату питающего напряжения. Для асинхронного двигателя также справедливы формулы (1.10) и (1.14). При решении задач нужно помнить, что при схеме соединения обмоток статора «звезда» фазные и линейные токи равны, а фазное напряжение в |




 , (1.1)
, (1.1) — частота вращения якоря, мин-1;
— частота вращения якоря, мин-1; — постоянная машины при расчете ЭДС.
— постоянная машины при расчете ЭДС. , (1.2)
, (1.2) — количество всех проводников в машине, шт.;
— количество всех проводников в машине, шт.;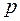 — количество пар полюсов, шт.;
— количество пар полюсов, шт.; — количество параллельных ветвей обмотки, шт.
— количество параллельных ветвей обмотки, шт. .
.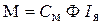 , (1.3)
, (1.3) — ток якоря, А;
— ток якоря, А; — постоянная машины при расчете момента,
— постоянная машины при расчете момента, . (1.4)
. (1.4)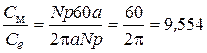 , (1.5)
, (1.5) , (1.6)
, (1.6) — напряжение генератора, В;
— напряжение генератора, В;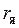 — сопротивление якоря, Ом;
— сопротивление якоря, Ом; , (1.7)
, (1.7) ; (1.8)
; (1.8) , (1.9)
, (1.9) . (1.10)
. (1.10)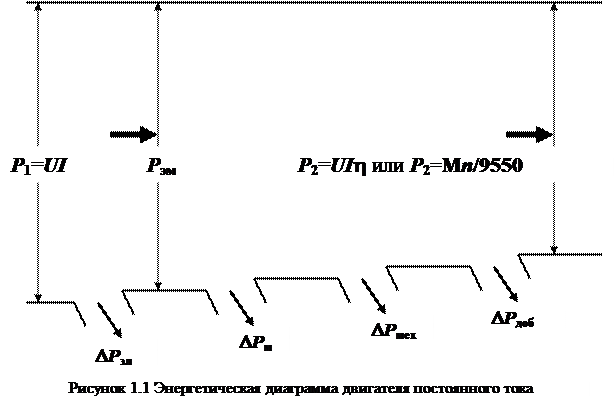
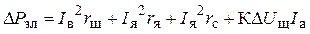 , (1.12)
, (1.12) — сопротивления соответственно обмоток параллельного возбуждения, якорной и последовательного возбуждения, Ом;
— сопротивления соответственно обмоток параллельного возбуждения, якорной и последовательного возбуждения, Ом; — падение напряжения на щётке, В;
— падение напряжения на щётке, В; — ток параллельной ветви, который идёт по щётке, А;
— ток параллельной ветви, который идёт по щётке, А; — количество щёток, шт.
— количество щёток, шт. (1.13)
(1.13) (1.14)
(1.14)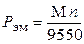 .
. .
. .
.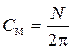 .
.
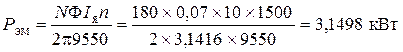
 .
. .
. .
.
 .
. Вб.
Вб. мин-1.
мин-1. и
и  определим ток якоря:
определим ток якоря: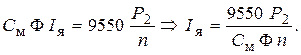
 . Получим
. Получим .
.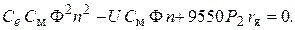
 ;
;  .
.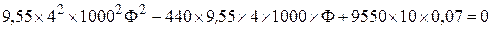
 (2.1)
(2.1)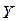 — расчетный шаг (равен полюсному делению, выраженному в зубцах);
— расчетный шаг (равен полюсному делению, выраженному в зубцах); — произвольное число меньше 1, доводящее расчетный шаг до целого числа.;
— произвольное число меньше 1, доводящее расчетный шаг до целого числа.; определяет число секций в катушечной группе и находится по формуле:
определяет число секций в катушечной группе и находится по формуле: (2.2)
(2.2)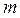 — число фаз;
— число фаз;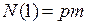 . (2.3)
. (2.3) ; (2.4)
; (2.4) ; (2.5)
; (2.5) , если нет, тогда число параллельных ветвей увеличивается.
, если нет, тогда число параллельных ветвей увеличивается. , (2.6)
, (2.6) , (2.7)
, (2.7) , (2.8)
, (2.8) ;
;  ,
,  , (2.9)
, (2.9) — угол укорочения, эл. град;
— угол укорочения, эл. град;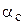 — угол скоса пазов.
— угол скоса пазов. , (2.10)
, (2.10) , (2.11)
, (2.11) — вектор реакции якоря по продольной оси, В;
— вектор реакции якоря по продольной оси, В; — вектор реакции якоря по поперечной оси, В;
— вектор реакции якоря по поперечной оси, В; — ЭДС, наводимая потоками рассеяния, В;
— ЭДС, наводимая потоками рассеяния, В; — вектор тока статора, А;
— вектор тока статора, А; — активное сопротивление обмотки статора, Ом.
— активное сопротивление обмотки статора, Ом. ;
;  ;
;  (2.12)
(2.12) ,
,  — составляющие тока статора соответственно по продольной и поперечной осям, А;
— составляющие тока статора соответственно по продольной и поперечной осям, А; — индуктивные сопротивления реакции якоря соответственно по продольной и поперечной осям, Ом;
— индуктивные сопротивления реакции якоря соответственно по продольной и поперечной осям, Ом; (2.13)
(2.13) где y1 — угол между вектором тока I1 и ЭДС E0, град. (см. рисунок 2.1).
где y1 — угол между вектором тока I1 и ЭДС E0, град. (см. рисунок 2.1). .
.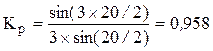 ;
; ,
,
 ;
;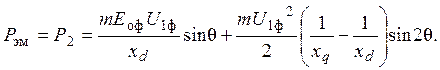
 В.
В.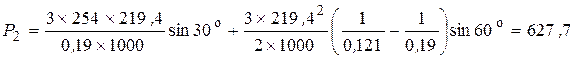 кВт.
кВт.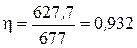
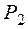 (Вт) можно определить по формуле:
(Вт) можно определить по формуле: , (3.1)
, (3.1)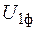 — фазное напряжение, подаваемое на двигатель, В;
— фазное напряжение, подаваемое на двигатель, В; — фазный ток статора, А;
— фазный ток статора, А;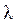 — коэффициент полезного действия.
— коэффициент полезного действия. , (3.2)
, (3.2) — частота вращения магнитного поля статора, мин-1;
— частота вращения магнитного поля статора, мин-1; , (3.3)
, (3.3)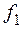 — частота тока, Гц;
— частота тока, Гц; — скольжение;
— скольжение;  .
.
 ;
;  ;
;  , (3.4)
, (3.4) ;
;  . (3.5)
. (3.5) ;
;  ;
;  , (3.6)
, (3.6) . (3.7)
. (3.7) , (3.8)
, (3.8) . (3.9)
. (3.9) раз меньше линейного; при схеме «треугольник» — наоборот: фазные и линейные напряжения равны, а фазный ток в
раз меньше линейного; при схеме «треугольник» — наоборот: фазные и линейные напряжения равны, а фазный ток в