 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Под действием постоянных сил.
Варианты 1 – 5 (рис. 1, схема 1). Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом, в течение τ (с). Его начальная скорость В точке B тело покидает плоскость со скоростью
горизонту, находясь в воздухе T (c). При решении задачи тело принять за материальную точку; сопротивление воздуха не учитывать. Вариант 1. Дано: α = 30º; β = 60°. Определить τ и h. Вариант 2. Дано: α = 15°; β = 45°. Определить l и уравнение траектории точки на участке ВС. Вариант 3. Дано: α = 30°; d = 10 м; β = 60°. Определить Вариант 4. Дано: Определить α и T. Вариант 5. Дано: α = 30°; Определить f и Варианты 6-10 (рис. 1, схема 2). Лыжник подходит к точке А участка АВ трамплина, наклоненного под углом а к горизонту и имеющего длину l, со скоростью При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха. Вариант 6. Дано: α = 20°; f = 0,1; τ = 0,2 с; h = 40 м; β = 30°. Определить l и Вариант 7. Дано: α = 15°; f = 0,1; β = 45°. Определить Вариант 8. Дано: β = 60°. Определить α и d. Вариант 9. Дано: α = 15°; τ = 0,3 с; f = 0,1; h = 30 β = 45°. Определить Вариант 10. Дано: α = 15°; f = 0; β = 60°. Определить τ и уравнение траектории лыжника на участке ВС. Варианты 11-15 (рис. 1, схема 3). Имея в точке А скорость мотоцикл поднимается τ (с) по участку АВ длиной l, составляющему с горизонтом угол α. При постоянной на всем участке АВ движущей силе Р мотоцикл в точке В приобретает скорость При решении задачи считать мотоцикл с мотоциклистом материальной точкой и не учитывать сил сопротивления движению. Вариант 11. Дано: α = 30°; P ≠ 0; l = 40м;
Вариант 12. Дано: α = 30°; Р = 0; l = 40 м; h = 1,5 м. Определить Вариант 13. Дано: α = 30°; m = 400 кг; d = 3 м; h = 1,5 м. Определить Р и l. Вариант 14. Дано: α = 30°; m = 400 кг; Р = 2,2 кН; l = 40 м; d = 5 м. Определить Вариант 15. Дано: α = 30°; h = 2 м; d = 4 м. Определить T и m. Варианты 16-20 (рис. 1, схема 4). Камень скользит в течение τ (с) по участку АВ откоса, составляющему угол α с горизонтом и имеющему длину l. Его начальная скорость Вариант 16. Дано: α = 30°; d = 2,5 м. Определить h и Т. Вариант 17. Дано: α = 45°; l = 6 м; =6 м. Определить d и f. Вариант 18. Дано: α = 30°; l = 2 м; Определить h и τ. Вариант 19. Дано: α =15°; l = 3 м; d = 2 м. Определить Вариант 20. Дано: α = 45°, Определить l и τ. Варианты 21-25 (рис. 1, схема 5). Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом. Его начальная скорость При решении задачи принять тело за материальную точку и не учитывать сопротивление воздуха. Вариант 21. Дано: α =30°; f = 0,1; h = 10 м. Определить Вариант 22. Дано: Определить f и уравнение траектории на участке ВС. Вариант 23. Дано: f = 0; Определить α и T. Вариант 24. Дано: h = 12 м. Определить τ и h. Вариант 25. Дано: h = 4,5 м. Определить τ и Варианты 26-30 (рис. 1, схема 6). Имея в точке А скорость Вариант 26. Дано: Определить d и Вариант 27. Дано: Определить Вариант 28. Дано: Определить Вариант 29. Дано: Определить f и d. Вариант 30. Дано: f = 0,25; l = 4 м; d = 3 м; h = 5 м. Определить Пример выполнения задания (рис. 2).Имея в точке А скорость
ку длиной l , составляющему с горизонтом угол Дано: α = 30º; Решение. Объект исследования – мотоциклист вместе с мотоциклом. При движении по участку АВ на объект действуют следующие силы: сила тяжести
Интегрируя это дифференциальное уравнение, получим:
Для определения постоянных интегрирования С1 и С2 подставим начальные условия ( Тогда из уравнений (2) и (3) найдем
Для момента времени
Рассмотрим движение объекта на криволинейном участке ВС. В этом случае на объект действует только сила тяжести
Интегрирование уравнения (8) дает:
Подставляя сюда соответствующие начальные условия Тогда
Интегрируя дифференциальное уравнение (9), имеем:
Окончательно
Поскольку координаты объекта в момент приземления
Из последних двух уравнений этой системы получим:
Откуда
а из первых двух уравнений системы определим скорость
Из уравнений (6), (7) следует, что = 40,43 с, а = 1,999·10³ H = 2,0 кН О т в е т: Задание Д-2.Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
Найти уравнения движения тела М массой m (рис. 3−5), принимаемого за материальную точку и находящегося под действием переменной силы Необходимые для решения данные 30-ти вариантов задания приведены в табл. 1, в которой приняты следующие обозначения: Во всех случаях, где сила Пример выполнения задания ( рис.6). Дано: Найти уравнение движения объекта. Решение. Объект исследования находится под действием силы тяжести Составим дифференциальное уравнение движения объекта:
Поскольку
или после подстановки исходных данных
Проинтегрируем полученное дифференциальное уравнение с помощью метода разделения переменных. Для этого уравнение (1) приведем к виду :
Далее , разделив переменные, получим:
Интегрируя это дифференциальное уравнение в заданных пределах, последовательно будем иметь:
и, наконец,
Разделим переменные в последнем дифференциальном уравнении и проинтегрируем в соответствующих пределах
Откуда искомое уравнение движения объекта получает вид:
Интегрирование дифференциального уравнения (1) можно выполнить и с помощью теории линейных дифференциальных уравнений, представив его в виде:
Уравнение (2) является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами, поэтому его общее решение отыскивается в форме:
где Для определения
Поскольку корни этого характеристического уравнения
Частное решение Тогда общее решение дифференциального уравнения (2) принимает вид:
Дифференцируя уравнение (3) по времени, будем иметь:
Подставляя в уравнения (3) и (4) начальные условия (
откуда определим постоянные интегрирования:
Подставив найденные значения постоянных интегрирования в общее решение (3), найдем искомое уравнение движения объекта:
Задание Д-З. Исследование колебательного движения материальной точки
Варианты 1-5 (рис. 7). Найти уравнение движения груза D массой Вариант 1. Груз D ( В некоторый момент времени к грузу D подвешивают груз Е ( Массой абсолютно жесткого бруска АВ и массой части демпфера, прикрепленной к бруску, пренебречь. Вариант2. В момент, когда стержень, соединяющий грузы D ( Вариант 3. Груз D ( В некоторый момент времени к грузу D подвешивают груз Е (
Вариант 4. Статическая деформация двух одинаковых параллельных пружин под действием грузов D ( Вариант 5. Одновременно с подвешиванием к грузу D ( Примечание. Положение начала отсчета на оси хсоответствует среднему положению точки В(ξ= 0). Варианты 6-10 (рис.7). Найти уравнение движения груза D массой т по гладкой наклонной плоскости, составляющей с горизонтом угол α, с момента соприкосновения груза с пружиной или с системой пружин, предполагая, что при дальнейшем движении груз от пружин не отделяется. Движение груза отнести к оси х, приняв за начало отсчета положение покоя груза (при статической деформации пружин). Вариант 6. Пройдя без начальной скорости по наклонной плоскости (α = 30°) расстояние s = 0,1 м, груз D ( Вариант 7. В некоторый момент времени груз D (т = 2 кг) присоединяют без начальной скорости к концу А недеформированных последовательно соединенных пружин, имеющих коэффициенты жесткости с1 = 12 Н/см, с2 = 6 Н/см. В тот же момент времени (t = 0) другой конец пружин В начинает совершать движение вдоль наклонной плоскости (α = 45°) по закону Примечание. Положение начала отсчета на оси хсоответствует среднему положению точки В(ξ= 0). Вариант 8. Две параллельные пружины 1 и 2, имеющие коэф- фициенты жесткости с1 = 4 Н/см и с2 = 6 Н/см, соединены абсолютно жестким бруском АВ, к точке К которого прикреплена пружина 3 с коэффициентом жесткости с3 = 15 Н/см. Точка К находится на расстояниях а и b от осей пружин 1 и 2: а/b = с2/с1. Пружины 1, 2 и 3 не деформированы. Груз D массой 1,5 кг присоединяют к концу N пружины 3; в тот же момент грузу D сообщают скорость Вариант 9. Груз D (т = 1,2 кг), пройдя без начальной скорости по наклонной плоскости (α = 30°) расстояние s = 0,2 м, ударяется о недеформированную пружину, коэффициент жесткости которой с = 4,8 Н/см. В этот же момент (t = 0) точка В (нижний конец пружин) начинает совершать вдоль наклонной плоскости движение по закону Вариант 10. Груз D (т = 1 кг) прикрепляют в середине абсолютно жесткого бруска АВ, соединяющего концы двух одинаковых параллельных пружин, не сообщая начальной скорости; пружины не деформированы. Коэффициент жесткости пружин с = 1,5 Н/см. Сопротивление движению груза пропорционально скорости: где v – скорость (м/с), α = 60°. Массой бруска АВ и массой части демпфера, прикрепленной к бруску, пренебречь. Варианты 11 - 15 (рис. 8). Груз D, массой т укреплен на конце невесомого стержня, который может вращаться в горизонтальной плоскости вокруг оси Е. Груз соединен с пружиной или с системой пружин; положение покоя стержня, показанное на чертеже, соответствует недеформированным пружинам. Считая, что груз D, принимаемый за материальную точку, движется по прямой, определить уравнение движения этого груза (трением скольжения груза по плоскости пренебречь). Движение отнести к оси х, за начало отсчета принять точку, соответствующую положению покоя груза. Вариант 11. Груз D (т = 2,4 кг) соединен с точкой F бруска АВ, связывающего концы двух параллельных пружин, коэффициенты жесткости которых с1= 1 Н/см и с2 = 1,4 Н/см. Точка F находится на расстояниях а и b от осей пружин: a/b = c2/с1. Груз D отклоняют на величину λ = 2 см влево от положения, показанного на чертеже, и отпускают без начальной скорости. Сопро-
тивление движению груза пропорционально скорости: v – скорость (м/с). Массой абсолютно жесткого бруска АВ и массой демпфера пренебречь. Вариант 12. В некоторый момент времени груз D (т = 3 кг), удерживаемый в положении, при котором пружина сжата на величину Примечание. Положение начала отсчета на оси хсоответствует среднему положению точки В(ξ= 0). Вариант 13. Груз D (т = 1 кг) прикреплен к концу пружины, имеющей коэффициент жесткости с1= 12 Н/см и соединенной другим концом с точкой F бруска АВ. Брусок АВ связывает концы двух параллельных пружин, коэффициент жесткости каждой из которых с = 3 Н/см. Точка F находится на равных расстояниях от осей параллельных пружин. Грузу в положении стержня, показанном на чертеже, сообщают скорость Сопротивление движению груза пропорционально скорости Шток демпфера пропущен через отверстие в невесомом бруске АВ и соединен с грузом D. Вариант 14. Груз D (т = 1,5 кг) прикреплен одной стороной к концу пружины, имеющей коэффициент жесткости с1 = 4,4 Н/см, а другой стороной − к концу двух последовательно соединенных пружин, коэффициенты жесткости которых с2 = 2 Н/см, с3 = 8 Н/см. Груз отклоняют на величину λ = 2,5 см влево от его положения, показанного на чертеже, и отпускают, одновременно сообщая грузу начальную скорость Вариант 15. Груз D (т = 1 кг) прикреплен к концу А последовательно соединенных пружин. Другой конец пружин В движется по закону Варианты 16−20 (рис. 8). Найти уравнение движения груза D массой грузов D и Е (при статической деформации пружин). Предполагается, что грузы D и Е при совместном движении не отделяются. Вариант 16. Пружина 1, на которой покоится груз D ( Массой абсолютно жесткого бруска АВ пренебречь. Вариант 17. В некоторый момент времени груз Е снимают с груза D (оба груза находятся в состоянии покоя, соответствующем статической деформации пружины). Круговая частота собственных колебаний системы грузов D и Е на пружине Вариант 18. Статическая деформация каждой из двух одинаковых параллельных пружин под действием груза D ( нально скорости: Вариант 19. Два груза D и Е ( Примечание. Положение начала отсчета на оси хсоответствует среднему положению точки В (ξ= 0). Вариант 20. На груз D, находящийся в состоянии покоя, соответствующем статической деформации пружины, в некоторый момент времени устанавливают груз Е. В этот же момент времени системе двух грузов сообщают скорость Варианты 21 − 25 (рис. 9). Найти уравнение движения груза D массой т по гладкой наклонной плоскости, составляющей с горизон- том угол α, отнеся движение к оси х; за начало отсчета принять положение покоя груза (при статической деформации пружин). Вариант 21. В некоторый момент времени груз D (т = 2 кг) прикрепляют к концам недеформированных пружин, имеющих коэффициенты жесткости с1 = 7 Н/см и с2 = 3 Н/см; одновременно грузу сообщают скорость Вариант 22. Груз D находится на наклонной плоскости (α = 30°) в состоянии покоя, соответствующем статической деформации пружины fст= 2 см. В некоторый момент времени (t = 0) точка В (верхний конец пружины) начинает совершать движение по закону Примечание. Положение начала отсчета на оси хсоответствует среднему положению точки В (ξ= 0). Вариант 23. Груз D (т = 3 кг) прикрепляют к точке F бруска АВ, соединяющего концы двух недеформированных параллельных пружин, и отпускают без начальной скорости. Коэффициенты жесткости пружин с1 = 2 Н/см и с2 = 4 Н/см. Точка F находится на расстояниях а и b от осей пружины: a/b = c2/с1; α = 60°. Сопротивление движению груза пропорционально скорости: Вариант 24. В некоторый момент времени груз D (т = 1 кг) прикрепляют к концу А недеформированных последовательно соединенных пружин, имеющих коэффициенты жесткости с1 = 12 Н/см и с2 = 4 Н/см, и отпускают без начальной скорости. Одновременно (t = 0) другой конец пружин В начинает совершать движение по закону Вариант 25. Концы двух одинаковых параллельных пружин соединены бруском АВ. Статическая деформация каждой из пружин под действием груза D (т =1,5 кг), находящегося на наклонной плоскости (α = 30°), fст = 4,9 см. В некоторый момент грузу D сооб-
щают скорость Массой абсолютно жесткого бруска АВ и массой части демпфера, связанной с бруском, пренебречь. Варианты 26−30 (рис. 9).Пренебрегая массой плиты и считая ее абсолютно жесткой, найти уравнение движения груза D массой т с момента соприкосновения его с плитой, предполагая, что при дальнейшем движении груз от плиты не отделяется. Движение груза отнести к оси х, приняв за начало отсчета положение покоя этого груза (при статической деформации пружин). Вариант 26. Плита лежит на двух параллельных пружинах, имеющих коэффициенты жесткости с1 = 600 Н/см и с2 = 400 Н/см. Груз D (m = 50 кг) падает без начальной скорости с высоты h = 0,1 м в точку F плиты, находящуюся на расстояниях a и b от осей пружин: а/b = с2/с1. Вариант 27. Коэффициент жесткости каждой из двух параллельных пружин, на которых лежит плита, с = 130 Н/см. Груз D (т = =40 кг) устанавливают на середину плиты и отпускают без начальной скорости при недеформированных пружинах. Сопротивление движению груза пропорционально скорости: R = 400 v (H), где v – скорость (м/с). Массой плиты и демпфера пренебречь. Вариант 28. Груз D падает на плиту с высоты h = 5 см. Статический прогиб пружины под действием этого груза fст = 1 см. Вариант 29. Плита лежит на двух одинаковых параллельных пружинах 1 и 2, коэффициенты жесткости которых с1= с2 = с = 400 Н/см. В некоторый момент времени груз D (т = 200 кг) устанавливают на середину плиты и одновременно прикрепляют к недеформированной пружине 3, имеющей коэффициент жесткости с3 = 200 Н/см. В тот же момент времени (при недеформированных пружинах) грузу сообщают скорость Вариант 30. В некоторый момент времени груз D (т = 100 кг) устанавливают на плиту и отпускают (при недеформированной пружине) без начальной скорости. В этот же момент времени точка В (нижний конец пружины) начинает совершать движение по вертикали согласно закону Примечание. Положение начала отсчета на оси хсоответствует среднему положению точки В(ξ= 0). Во всех вариантах задания после выполнения расчетных операций построить с помощью компьютера график исследуемого процесса Пример выполнения задания (рис. 10). Груз D ( Решение. Поскольку груз D совершает прямолинейное поступательное движение, его можно рассматривать как материальную точку. Направим ось В текущий момент времени
Здесь
При этом дифференциальное уравнение (1) примет вид
Рис. 10
или после преобразования
Введя обозначения
приведем дифференциальное уравнение к следующему виду:
Общее решение этого линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами складывается из общего решения Найдем числовые значения входящих в дифференциальное уравнение (3) величин: Поскольку n<k , корни соответствующего характеристического уравнения
где Частное решение дифференциального уравнения (3) описывает вынужденные колебания груза
где
амплитуда вынужденных колебаний;
Общее решение исходного дифференциального уравнения (3) принимает вид
Для определения постоянных интегрирования
+ и, используя начальные условия задачи, получим:
откуда
Подставляя найденные постоянные интегрирования
или с учетом найденных значений входящих в уравнение (6) величин
На рис. 11, а представлен график ных гармонических колебаний (рис.11, б) и собственных затухающих колебаний Отметим, что при отсутствии демпфирования
В этом слу |



 . Коэффициент трения скольжения тела по плоскости равен f.
. Коэффициент трения скольжения тела по плоскости равен f. и попадает со скоростью
и попадает со скоростью  в точку C плоскости BD, наклоненной под углом β к
в точку C плоскости BD, наклоненной под углом β к Рис.1
Рис.1 и τ.
и τ. = 0; τ = 2 с; l = 9,8 м; β = 60°; f = 0.
= 0; τ = 2 с; l = 9,8 м; β = 60°; f = 0.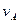 . Коэффициент трения скольжения лыж на участке АВ равен f. Лыжник от A до В движется τ (с); в точке В со скоростью
. Коэффициент трения скольжения лыж на участке АВ равен f. Лыжник от A до В движется τ (с); в точке В со скоростью  м;
м; и d.
и d. (с) по прямолинейному участ-
(с) по прямолинейному участ- Рис. 2
Рис. 2 . При постоянной на всем участке АВ движущей силе P мотоциклист в точке B приобретает скорость
. При постоянной на всем участке АВ движущей силе P мотоциклист в точке B приобретает скорость  , движущая сила
, движущая сила  и нормальная реакция
и нормальная реакция 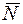 наклонной плоскости. Составим дифференциальное уравнение движения объекта на рассматриваемом участке:
наклонной плоскости. Составим дифференциальное уравнение движения объекта на рассматриваемом участке: ;
;  (1)
(1) (2)
(2) (3)
(3)
 в уравнения (2) и (3). Откуда
в уравнения (2) и (3). Откуда  т. е.
т. е. 
 (4)
(4)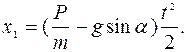 (5)
(5) из уравнений (4) и (5) получим :
из уравнений (4) и (5) получим : (6)
(6) (7)
(7) (8)
(8) (9)
(9) .
. , определяем постоянные интегрирования
, определяем постоянные интегрирования  и
и  :
:  , т. е.
, т. е.  .
. ; (10)
; (10) (11)
(11) (12)
(12)  (13) Используя начальные условия
(13) Используя начальные условия  , из уравнений (12) и (13) получим:
, из уравнений (12) и (13) получим:  , т. е.
, т. е.  ;
;  .
. (14)
(14) (15)
(15) в точке С
в точке С 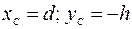 , для этого момента времени из уравнений (10), (11), (14) и (15) следует:
, для этого момента времени из уравнений (10), (11), (14) и (15) следует: ;
;



 м/с ;
м/с ; с,
с, с
с м/с;
м/с; м/с;
м/с;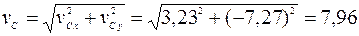 м/с.
м/с. =2·
=2·  =
= =
= кH;
кH;  с;
с;  с;
с;  м/с ;
м/с ;  м/с.
м/с. , при заданных начальных условиях. Во всех вариантах ось z (где показана) вертикальна, за исключением вариантов 8 и 30.
, при заданных начальных условиях. Во всех вариантах ось z (где показана) вертикальна, за исключением вариантов 8 и 30. − орты координатных осей (соответственно
− орты координатных осей (соответственно 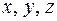 );
);  − ускорение свободного падения (9,81 м/с2); ƒ − коэффициент трения скольжения; t − время, с;
− ускорение свободного падения (9,81 м/с2); ƒ − коэффициент трения скольжения; t − время, с;  − координаты точки и проекции ее скорости на оси координат соответственно, м и м/с.
− координаты точки и проекции ее скорости на оси координат соответственно, м и м/с. зависит от
зависит от  , рассмотреть движение объекта, при котором эти величины только положительны.
, рассмотреть движение объекта, при котором эти величины только положительны. =2 кг;
=2 кг;  ,
,  =0,6 Н·с/м;
=0,6 Н·с/м;  =0,2;
=0,2;  =0;
=0;  =4 м/с.
=4 м/с. .
. .
.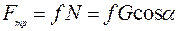 , а
, а  , это дифференциальное уравнение приобретает вид:
, это дифференциальное уравнение приобретает вид:
 . (1)
. (1) .
. Рис. 3
Рис. 3 Рис. 4
Рис. 4 Рис. 5
Рис. 5
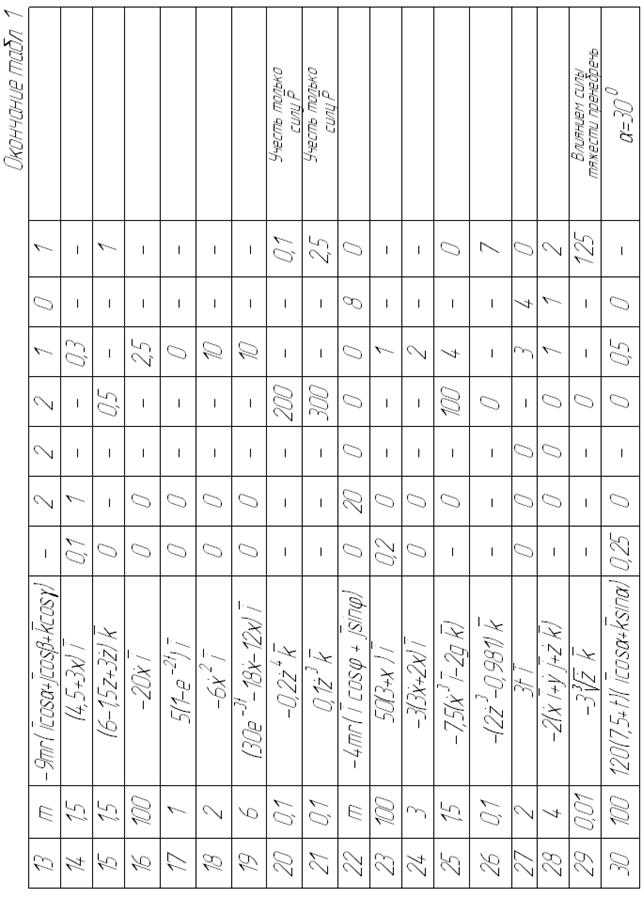
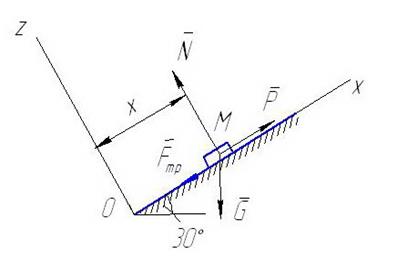 Рис. 6
Рис. 6 .
. ,
, ,
,  │
│  =−
=−  ,
, =−
=− 
 ,
, 
 , м/с.
, м/с. ,
, ,
,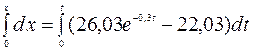 ,
, │
│ 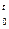 −22,03
−22,03  │
│  , м.
, м. .
.  ,
, − общее решение однородного дифференциального уравнения
− общее решение однородного дифференциального уравнения  , а
, а  − частное решение неоднородного уравнения (2).
− частное решение неоднородного уравнения (2). .
.
 являются действительными неравными числами, общее решение
являются действительными неравными числами, общее решение  , т. е.
, т. е.  .
. . Подставляя
. Подставляя  м/с.
м/с. . (3)
. (3) . (4)
. (4) м/с), получим:
м/с), получим: ;
; 
 м,
м, м.
м. (варианты 2 и 4) или системы грузов D и Е массами
(варианты 2 и 4) или системы грузов D и Е массами  (варианты 1, 3, 5), отнеся их движение к оси х; начало отсчета совместить с положением покоя груза D или соответственно системы грузов D и Е (при статической деформации пружин). Стержень, соединяющий грузы, считать невесомым и недеформируемым.
(варианты 1, 3, 5), отнеся их движение к оси х; начало отсчета совместить с положением покоя груза D или соответственно системы грузов D и Е (при статической деформации пружин). Стержень, соединяющий грузы, считать невесомым и недеформируемым. (Н), где v - скорость (м/с).
(Н), где v - скорость (м/с). (см) (ось
(см) (ось  направлена вертикально вниз). Коэффициенты жесткости пружин с1 = 12 Н/см, с2 = 36 Н/см.
направлена вертикально вниз). Коэффициенты жесткости пружин с1 = 12 Н/см, с2 = 36 Н/см. = 0,2 м/с, направленную вниз. Массой абсолютно жесткого бруска АВ пренебречь.
= 0,2 м/с, направленную вниз. Массой абсолютно жесткого бруска АВ пренебречь. (Н), где v – скорость (м/с). Массой бруска АВ и массой части демпфера, прикрепленной к бруску, пренебречь.
(Н), где v – скорость (м/с). Массой бруска АВ и массой части демпфера, прикрепленной к бруску, пренебречь. (см) (ось ξ направлена вертикально вниз).
(см) (ось ξ направлена вертикально вниз). (м) (ось ξ направлена вдоль наклонной плоскости вниз).
(м) (ось ξ направлена вдоль наклонной плоскости вниз). (м) (ось ξ направлена вдоль наклонной плоскости вниз) (см. примечание к варианту 7).
(м) (ось ξ направлена вдоль наклонной плоскости вниз) (см. примечание к варианту 7). (H),
(H), Рис.7
Рис.7 Рис. 8
Рис. 8 (H), где
(H), где = 2 см, отпускают без начальной скорости. Коэффициент жесткости пружины с=9 Н/см. Одновременно ( t=0 ) точка B ( правый конец пружины) начинает совершать движение по закону
= 2 см, отпускают без начальной скорости. Коэффициент жесткости пружины с=9 Н/см. Одновременно ( t=0 ) точка B ( правый конец пружины) начинает совершать движение по закону  (см) (ось ξ направлена влево).
(см) (ось ξ направлена влево). (H), где v – скорость (м/с).
(H), где v – скорость (м/с). (см) (ось ξ направлена влево). Коэффициенты жесткости пружин с1 = 4 Н/см, с2 = 12 Н/см. При t = 0 груз находился в положении покоя, соответствующем недеформированным пружинам (см. примечание к варианту 12).
(см) (ось ξ направлена влево). Коэффициенты жесткости пружин с1 = 4 Н/см, с2 = 12 Н/см. При t = 0 груз находился в положении покоя, соответствующем недеформированным пружинам (см. примечание к варианту 12). = 200 Н/см,
= 200 Н/см, 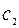 = 160 Н/см,
= 160 Н/см,  = 140 Н/см. Точка F находится на расстояниях а и b от осей пружин 2 и 3: а/b =
= 140 Н/см. Точка F находится на расстояниях а и b от осей пружин 2 и 3: а/b =  = 20 рад/с, отношение масс
= 20 рад/с, отношение масс  = 2 см. В некоторый момент времени на груз D устанавливают груз Е (
= 2 см. В некоторый момент времени на груз D устанавливают груз Е (  (H), где v – скорость (м/с). Массой абсолютно жесткого бруска АВ и массой части демпфера, связанной с ним, пренебречь.
(H), где v – скорость (м/с). Массой абсолютно жесткого бруска АВ и массой части демпфера, связанной с ним, пренебречь. (см) (ось ξ направлена вертикально вниз).
(см) (ось ξ направлена вертикально вниз).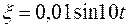 (м) (ось ξ направлена вдоль наклонной плоскости вниз).
(м) (ось ξ направлена вдоль наклонной плоскости вниз). (см). Ось ξ направлена вдоль наклонной плоскости вниз (α = 30°) (см. примечание к варианту 22).
(см). Ось ξ направлена вдоль наклонной плоскости вниз (α = 30°) (см. примечание к варианту 22). Рис. 9
Рис. 9 (м/с), направленную вниз.
(м/с), направленную вниз. (см) (ось ξ направлена вниз). Коэффициент жесткости пружины с = 2000 Н/см.
(см) (ось ξ направлена вниз). Коэффициент жесткости пружины с = 2000 Н/см. движения груза (или грузов).
движения груза (или грузов). 30° к горизонту. Коэффициент жесткости пружины, удерживающей груз,
30° к горизонту. Коэффициент жесткости пружины, удерживающей груз,  8 Н/см. В некоторый момент времени точка B (левый конец пружины) начинает совершать движение согласно закону
8 Н/см. В некоторый момент времени точка B (левый конец пружины) начинает совершать движение согласно закону  (см) (ось
(см) (ось  , полагая, что сила сопротивления движению, осуществляемая гидравлическим демпфером, пропорциональна скорости груза: R = 8v (H), где v – скорость (м/с). Начало отсчета на оси
, полагая, что сила сопротивления движению, осуществляемая гидравлическим демпфером, пропорциональна скорости груза: R = 8v (H), где v – скорость (м/с). Начало отсчета на оси  ;
; 
 ;
;  .
. пружины и сила сопротивления
пружины и сила сопротивления  демпфера (рис. 10, б). Прямолинейное движение груза вдоль оси x описывается следующим дифференциальным уравнением:
демпфера (рис. 10, б). Прямолинейное движение груза вдоль оси x описывается следующим дифференциальным уравнением: . (1)
. (1) , где
, где  − длины пружины в текущем и недеформированном состояниях соответственно;
− длины пружины в текущем и недеформированном состояниях соответственно;  − статическая деформация пружины (в состоянии покоя груза
− статическая деформация пружины (в состоянии покоя груза  и
и  , т.е.
, т.е.  и
и  , откуда
, откуда  );
);  (b =1,5 см;
(b =1,5 см;  18 рад/с) – перемещение точки B пружины;
18 рад/с) – перемещение точки B пружины; 
 (
(  8Н·с/м − коэффициент сопротивления демпфера).
8Н·с/м − коэффициент сопротивления демпфера). (2)
(2)
 .
. ,
, 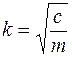 ,
,  ,
, . (3)
. (3)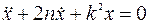 и частного решения
и частного решения  с-1 – коэффициент затухания;
с-1 – коэффициент затухания;  рад/с
рад/с  20с-1 – круговая частота собственных незатухающих колебаний груза;
20с-1 – круговая частота собственных незатухающих колебаний груза; 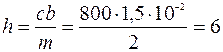 м/с2 –относительная амплитуда кинематического возбуждения колебаний.
м/с2 –относительная амплитуда кинематического возбуждения колебаний. являются комплексно-сопряженны- ми числами
являются комплексно-сопряженны- ми числами  ,9i и общее решение
,9i и общее решение  ,
, 19,9 рад/с – круговая частота собственных затухающих колебаний груза.
19,9 рад/с – круговая частота собственных затухающих колебаний груза. ,
, 0,057 м –
0,057 м – 0,758 рад – сдвиг фазы вынужденных колебаний относительно фазы кинематического возбуждения.
0,758 рад – сдвиг фазы вынужденных колебаний относительно фазы кинематического возбуждения. . (4)
. (4) и
и  формируем, кроме того, функцию
формируем, кроме того, функцию +
+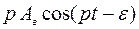 (5)
(5)
 ,
, м;
м; м.
м. (6)
(6) , м. (7)
, м. (7) исследуемого процесса движения
исследуемого процесса движения  с частотой
с частотой  рад/с
рад/с с частотой
с частотой  рад/с (рис.11, в).
рад/с (рис.11, в).

 рад/с;
рад/с;  м;
м;  .
.