 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Задание Д-5. Применение общих теорем динамики
К исследованию движения материальной точки Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которой расположена в вертикальной плоскости (рис. 17−21). Найти скорость шарика  и и  в положениях В и С и силу давления в положениях В и С и силу давления 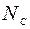 шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь  , отделяется от пружины. , отделяется от пружины. Необходимые для решения данные приведены в табл. 3. В задании приняты следующие обозначения: т− масса шарика;  − начальная скорость шарика; − начальная скорость шарика;  − время движения шарика на участке АВ ( в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке ВD (в вариантах 3, 4, 6, 7, − время движения шарика на участке АВ ( в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке ВD (в вариантах 3, 4, 6, 7, 9−13, 15−17, 19, 22, 25, 26, 28, 29);  − коэффициент трения − коэффициент трения  Рис. 17 Рис. 17
 Рис. 18 Рис. 18

Рис. 19 
Рис. 20  Рис. 21 Рис. 21


скольжения шарика по стенке трубки;  − начальная деформация пружины; h – наибольшее сжатие пружины; с − коэффициент жесткости пружины; Н − наибольшая высота подъема шарика; s − путь, пройденный шариком до остановки. − начальная деформация пружины; h – наибольшее сжатие пружины; с − коэффициент жесткости пружины; Н − наибольшая высота подъема шарика; s − путь, пройденный шариком до остановки. Пример выполнения задания (рис. 22).Дано: т= 0,5 кг,  м/с; м/с;  = 0,2 с (время движения на участке ВD); R=0,4 м; = 0,2 с (время движения на участке ВD); R=0,4 м;  0,1; 0,1;  = 45°; = 45°;  = 60°; = 60°;  = 0; с = 20 Н/см = 2000 Н/м. = 0; с = 20 Н/см = 2000 Н/м. Определить  , ,  , , 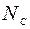 , ,  , ,  . . Решение. Для определения  и и  применим теорему об изменении кинетической энергии материальной точки. Движение шарика на участках АС и АВ траектории происходит под действием силы тяжести применим теорему об изменении кинетической энергии материальной точки. Движение шарика на участках АС и АВ траектории происходит под действием силы тяжести  (силы трения на криволинейных участках не учитываем): (силы трения на криволинейных участках не учитываем):  °); °);   ; ;
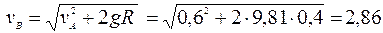 м/с; м/с;
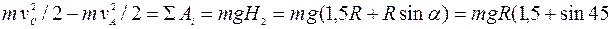 °); °);
 ; ;
 м/с. м/с.
Определим силу давления шарика на стенку трубки в положении С. На шарик в этом случае действует сила тяжести  и сила реакции и сила реакции  стенки трубки (рис. 22, б). Записав основное уравнение динамики материальной точки в проекциях на главную нормаль стенки трубки (рис. 22, б). Записав основное уравнение динамики материальной точки в проекциях на главную нормаль  к траектории шарика в точке С, будем иметь: к траектории шарика в точке С, будем иметь: 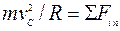 ; ;  . .
Отсюда  Н. Н.
Искомая сила давления  шарика на стенку трубки по модулю равна найденной реакции шарика на стенку трубки по модулю равна найденной реакции  и направлена в противоположную сторону ( и направлена в противоположную сторону (  . . Скорость шарика в положении D при его движении на участке BD траектории найдем с помощью теоремы об изменении количества движения материальной точки, записав ее в проекциях на ось  рис. 22, в):  , (1) , (1)
а) 
б) в) 
Рис. 22 где  − алгебраическая сумма проекций импульсов сил, приложен- − алгебраическая сумма проекций импульсов сил, приложен- ных к шарику за время его движения  (с) на рассматриваемом участке траектории. (с) на рассматриваемом участке траектории. Так как к шарику приложены сила тяжести  нормальная реакция нормальная реакция  и сила трения и сила трения  причем причем  , ,
то  . .
Тогда из уравнения (1) получим  , ,
откуда  м/с. м/с.
Величину максимального сжатия  пружины определим из условия: в положении E при максимальном сжатии пружины скорость шарика равна нулю ( пружины определим из условия: в положении E при максимальном сжатии пружины скорость шарика равна нулю (  ). Тогда на основании теоремы об изменении кинетической энергии материальной точки на участке ). Тогда на основании теоремы об изменении кинетической энергии материальной точки на участке  движения шарика будем иметь: движения шарика будем иметь:  , (2) , (2)
где  - алгебраическая сумма работ силы тяжести - алгебраическая сумма работ силы тяжести  силы упруго- силы упруго-
сти  нормальной реакции нормальной реакции  и силы трения и силы трения  , действующих на шарик на участке DE его траектории: , действующих на шарик на участке DE его траектории:  . Учитывая, что . Учитывая, что  , из уравнения (2) получим: , из уравнения (2) получим:  
или  . (3) . (3)
Решая квадратное уравнение (2) относительно величины  , получим: , получим:  
 м. м.
Откуда, поскольку величина  положительна, искомая величина максимального сжатия пружины положительна, искомая величина максимального сжатия пружины  м. м. Ответ:  м/с; м/с;  м/с; м/с;  м/с; м/с; 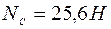 ; ;  =0,073 м. =0,073 м.
Динамика MЕХАНИЧЕСКОЙ СИСТЕМЫ ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МЕХАНИЧЕСКОЙ СИСТЕМЫ Задание Д-6. Применение теоремы об изменении Кинетического момента к определению
|




 и
и  в положениях В и С и силу давления
в положениях В и С и силу давления 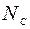 шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь
шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь  , отделяется от пружины.
, отделяется от пружины. − начальная скорость шарика;
− начальная скорость шарика;  − время движения шарика на участке АВ ( в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке ВD (в вариантах 3, 4, 6, 7,
− время движения шарика на участке АВ ( в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке ВD (в вариантах 3, 4, 6, 7, − коэффициент трения
− коэффициент трения Рис. 17
Рис. 17 Рис. 18
Рис. 18

 Рис. 21
Рис. 21

 м/с;
м/с;  0,1;
0,1;  = 45°;
= 45°;  = 60°;
= 60°;  ,
,  .
. (силы трения на криволинейных участках не учитываем):
(силы трения на криволинейных участках не учитываем): °);
°); 
 ;
;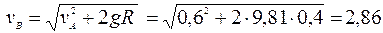 м/с;
м/с;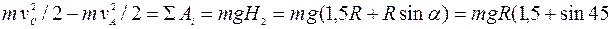 °);
°); ;
; м/с.
м/с. стенки трубки (рис. 22, б). Записав основное уравнение динамики материальной точки в проекциях на главную нормаль
стенки трубки (рис. 22, б). Записав основное уравнение динамики материальной точки в проекциях на главную нормаль  к траектории шарика в точке С, будем иметь:
к траектории шарика в точке С, будем иметь: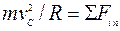 ;
;  .
. Н.
Н. шарика на стенку трубки по модулю равна найденной реакции
шарика на стенку трубки по модулю равна найденной реакции  .
.
 , (1)
, (1)

 − алгебраическая сумма проекций импульсов сил, приложен-
− алгебраическая сумма проекций импульсов сил, приложен- нормальная реакция
нормальная реакция  и сила трения
и сила трения  причем
причем ,
, .
. ,
, м/с.
м/с. ). Тогда на основании теоремы об изменении кинетической энергии материальной точки на участке
). Тогда на основании теоремы об изменении кинетической энергии материальной точки на участке  движения шарика будем иметь:
движения шарика будем иметь: , (2)
, (2) - алгебраическая сумма работ силы тяжести
- алгебраическая сумма работ силы тяжести  нормальной реакции
нормальной реакции  , действующих на шарик на участке DE его траектории:
, действующих на шарик на участке DE его траектории:  . Учитывая, что
. Учитывая, что  , из уравнения (2) получим:
, из уравнения (2) получим:
 . (3)
. (3)

 м.
м. положительна, искомая величина максимального сжатия пружины
положительна, искомая величина максимального сжатия пружины  м.
м. м/с;
м/с;  м/с;
м/с;  м/с;
м/с; 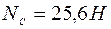 ;
;