 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вращательного движений твердого тела
Механическая система состоит из механизма (колес 1 и 2) и груза 3. К колесу 1 механизма приложена пара сил с моментом Время Массы колес 1 и 2механизма − Радиусы больших и малых окружностей колес 1 и 2: Схемы механизмов показаны на рис. 35−39, а необходимые для решения данные приведены в табл. 7. Найти уравнение движения тела системы, указанного в последнем столбце табл. 7. Определить
также силы натяжения нитей в заданный момент времени Пример выполнения задания (рис. 40).Дано: Найти уравнение Решение. Рассмотрим в качестве объекта исследования колесо 1 (рис. 40, б), которое находится под действием силы тяжести Дифференциальное уравнение вращения колеса 1
где При составлении
Рассмотрим колесо 2 и составим дифференциальное уравнение его вращения вокруг неподвижной оси
К колесу 2механизма приложены: сила тяжести
Рис. 40
ла натяжения
Тогда главный момент
и дифференциальное уравнение (4) примет вид
Выразим угловое ускорение Так как и дифференциальное уравнение (6) приобретает вид
Теперь рассмотрим в качестве объекта исследования груз 3, движущийся поступательно, и составим дифференциальное уравнение, описывающее его движение:
Здесь Так как к грузу приложены сила тяжести
кроме того, выразив ускорение груза через
что позволяет привести дифференциальное уравнение (8) движения груза к следующему виду:
Уравнения (3), (7), (9) составляют систему совместных дифференциальных уравнений
В этих уравнениях неизвестны силы S1= S2 = S и
и подставим во второе:
откуда
Затем умножим полученное уравнение на
Отсюда
Выражение (12) определяет в общем виде угловое ускорение колеса 1. Учитывая исходные данные, найдем моменты инерции колес 1 и 2 относительно осей
Тогда по формуле (12) получим:
Интегрируем это уравнение дважды:
Для определения постоянных интегрирования
Отсюда найдем, что
Окружное усилие
При
и тогда
Силу натяжения
Ответ: |



 (движущий момент) или движущая сила
(движущий момент) или движущая сила  .
. отсчитывается от некоторого момента (t = 0), в который угол поворота и угловая скорость колеса 1 равны соответственно:
отсчитывается от некоторого момента (t = 0), в который угол поворота и угловая скорость колеса 1 равны соответственно:  ,
,  . Момент сил сопротивления вращению ведомого колеса 2равен
. Момент сил сопротивления вращению ведомого колеса 2равен  . Другие силы сопротивления движению системы не учитывать.
. Другие силы сопротивления движению системы не учитывать. и
и  , а масса поднимаемого груза 3 −
, а масса поднимаемого груза 3 −  .
.
 Рис. 35
Рис. 35 Рис. 36
Рис. 36 Рис. 37
Рис. 37 Рис. 38
Рис. 38 Рис. 39
Рис. 39

 , а в вариантах, где имеется контакт колес 1 и 2,найти, кроме того, окружное усилие в точке их соприкосновения. Колеса 1 и 2,для которых радиусы инерции
, а в вариантах, где имеется контакт колес 1 и 2,найти, кроме того, окружное усилие в точке их соприкосновения. Колеса 1 и 2,для которых радиусы инерции  и
и  относительно их неподвижных осей вращения втабл. 7 не заданы, считать сплошными однородными дисками.
относительно их неподвижных осей вращения втабл. 7 не заданы, считать сплошными однородными дисками. кг;
кг;  кг; m3=400 кг;
кг; m3=400 кг;  Н;
Н;  Н·м = const;
Н·м = const;  см;
см;  см;
см;  см;
см;  см;
см;  рад/с.
рад/с. вращательного движения колеса 1механизма, а также окружное усилие
вращательного движения колеса 1механизма, а также окружное усилие  в точке контакта колес 1 и 2и силу натяжения T нитив момент времени t1= 2,5 с (рис. 40, а).
в точке контакта колес 1 и 2и силу натяжения T нитив момент времени t1= 2,5 с (рис. 40, а). , движущей силы
, движущей силы  , составляющих
, составляющих  ,
,  реакции подшипника
реакции подшипника  ,а также окружного
,а также окружного  и радиального
и радиального  усилий со стороны колеса 2.
усилий со стороны колеса 2. , (1)
, (1) момент инерции колеса относительно его неподвижной оси вращения
момент инерции колеса относительно его неподвижной оси вращения  ;
;  главный момент внешних сил , приложенных к колесу, относительно той же оси .
главный момент внешних сил , приложенных к колесу, относительно той же оси . учитывается следующее правило знаков моментов: момент движущей силы
учитывается следующее правило знаков моментов: момент движущей силы  , приводящий в движение колесо 1, является положительным, а момент силы
, приводящий в движение колесо 1, является положительным, а момент силы  , (2) и дифференциальное уравнение вращения колеса 1 примет вид:
, (2) и дифференциальное уравнение вращения колеса 1 примет вид: . (3)
. (3)
 (4)
(4) , момент сил сопротивления
, момент сил сопротивления  ,
,  реакции подшипника B ,си-
реакции подшипника B ,си-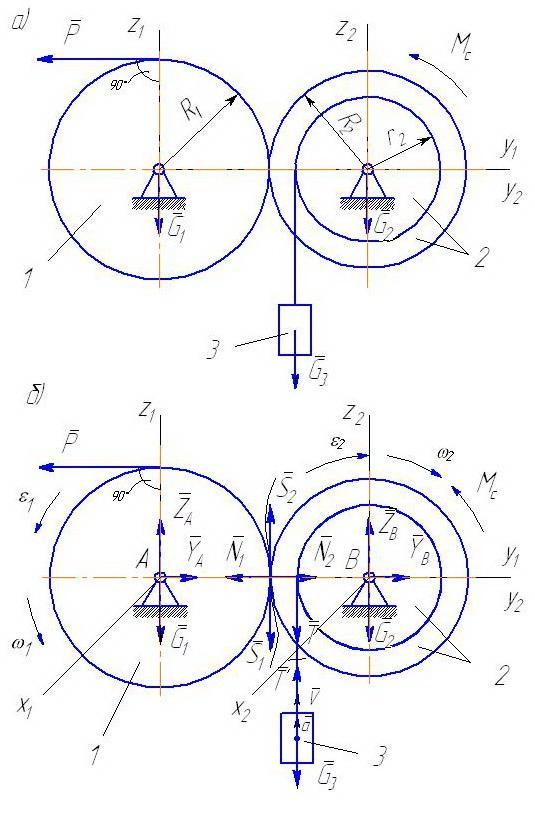
 нити, к которой подвешен груз 3,а также окружное
нити, к которой подвешен груз 3,а также окружное  и радиальное
и радиальное  усилия со стороны колеса 1. При этом очевидно:
усилия со стороны колеса 1. При этом очевидно: .
. , (5)
, (5) . (6)
. (6) колеса 2 через угловое ускорение
колеса 2 через угловое ускорение  колеса 1, уравнение вращения которого
колеса 1, уравнение вращения которого  , то
, то  ,
, . (7)
. (7) . (8)
. (8)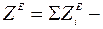 проекция главного вектора внешних сил, приложенных к грузу 3, на ось
проекция главного вектора внешних сил, приложенных к грузу 3, на ось  , направленную в сторону движения груза, т. е. вверх.
, направленную в сторону движения груза, т. е. вверх. и сила натяжения
и сила натяжения  нити (очевидно, что
нити (очевидно, что  , то
, то ,
, , получим:
, получим: ,
, . (9)
. (9) , а также угловое ускорение
, а также угловое ускорение  , для чего из третьего уравнения этой системы определим
, для чего из третьего уравнения этой системы определим (11)
(11) ,
, .
.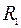 , а первое уравнение системы (10) на
, а первое уравнение системы (10) на  и, сложив соответствующие части уравнений, получим:
и, сложив соответствующие части уравнений, получим: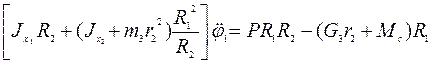 .
. . (12 )
. (12 ) кг·м2;
кг·м2;  кг·м2.
кг·м2.

 рад/с2 .
рад/с2 . (13)
(13) ;
; .
. и
и  начальные условия (
начальные условия (  рад/с) подставим в первый и второй интегралы
рад/с) подставим в первый и второй интегралы ;
; .
. рад/с;
рад/с;  , а следовательно, искомое уравнение вращения колеса 1 имеет следующий вид:
, а следовательно, искомое уравнение вращения колеса 1 имеет следующий вид: (рад). (14)
(рад). (14) .
. с угловое ускорение
с угловое ускорение  составит
составит рад/с2,
рад/с2, Н.
Н. Н.
Н. Н;
Н;  Н.
Н.