 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| координат к исследованию движения механической системы с одной степенью свободы
Для рассмотренных в задании Д-12 вариантов механической системы (рис. 60−64 ) с помощью метода обобщенных координат определить ускорения грузов и центров масс катков. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Необходимые для решения данные приведены в табл. 11. Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами.Все катки, включая и катки, обмотанные нитями, перемещаются по опорным поверхностям без скольжения. Пример выполнения задания (рис. 68).Дано:
Решение. Решим эту задачу методом обобщенных координат, воспользовавшись уравнением Лагранжа второго рода. Объект исследования − движущаяся механическая система, состоящая из груза 1, барабана 2 и катка 3, − имеет одну степень свободы. Выберем в качестве обобщенной координаты q линейное перемещение Тогда соответствующее уравнение Лагранжа будет иметь вид:
где Т –кинетическая энергия системы в ее абсолютном движении; Q –обобщенная сила, соответствующая выбранной обобщенной координате. Определим кинетическую энергию Т системы как сумму кинетических энергий всех тел, входящих в систему:
Так как груз 1 движется поступательно, барабан 2 вращается вокруг неподвижной оси, а каток 3 совершает плоское движение, то
где
Все входящие в выражение (3) скорости выразим через обобщенную скорость Очевидно, что
Рис. 68
Подставляя найденные значения скоростей, значения осевых моментов инерции
Далее находим
где, естественно, Теперь определим обобщенную силу Q . Изобразим на расчетной схеме действующие на систему активные силы: силу тяжести груза 1, силу тяжести Мысленно зафиксировав текущее положение системы, и во избежание ошибок в знаках, сообщим ей такое возможное перемещение, при котором обобщенная координата
где
Возможное перемещение
Тогда из выражения (4) следует:
Далее, сокращая числитель и знаменатель на
Подставив в уравнение (1) выражения
найдем
и
Ответ:
______________
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Сборник заданий для курсовых работ по теоретической механике/ под общей ред. А.А.Яблонского. – М.: Высш.шк., 2008. – 382 с. 2. Тарг, С.М. Краткий курс теоретической механики/ С.М. Тарг. – М.: Высш.шк., 2008. – 416 с. 3. Яблонский, А.А. Курс теоретической механики/ А.А. Яблонский, В.М. Никифорова. – М.: Интеграл-пресс, 2006. – 595с. 4. Теоретическая механика. Динамика материальной точки/ Е.И. Селенский, Т.В. Селенская: учебное пособие. – Брянск, БГТУ, 2004. – 68с. 5. Теоретическая механика. Динамика / Е.И. Селенский, Т.В. Селенская: методические указания. – Брянск, БГТУ, 2000. – 73с.
ОГЛАВЛЕНИЕ ПРЕДИСЛОВИЕ………………………………………………...... 3 ВВЕДЕНИЕ………………………………………………………... 4
1. Динамика материальной точки………………..4
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ………………………………………. 4 Задание Д-1. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил………………….. 4 Задание Д-2.Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил.............................. 12 Задание Д-З. Исследование колебательного движения материальной точки.………………………………. 20 Задание Д-4. Исследование динамики относительного движения материальной точки ………………….. 35 ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ…………………………………………………………….. 45 Задание Д-5. Применение общих теорем динамики к исследованию движения материальной точки….. 45
2. Динамика MЕХАНИЧЕСКОЙ СИСТЕМЫ………….. 56 ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МЕХАНИЧЕСКОЙ СИСТЕМЫ………………………………………………………… 56 Задание Д-6. Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела…………………………… 56 Задание Д-7. Применение теоремы об изменении кинетической энергии к изучению движения механической системы……………………………………………. 68 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА………………………………………………… 81 Задание Д-8. Исследование поступательного и вращательного движений твердого тела…………………………… 81 Задание Д-9. Исследование плоского движения твердого тела……………………………………………….... 94
3. ОБЩИЕ ПРИНЦИПЫ И МЕТОДЫ МЕХАНИКИ……... 105
ПРИНЦИП ДАЛАМБЕРА И МЕТОД КИНЕТОСТАТИКИ…... 105 Задание Д-10. Применение принципа Даламбера к определению реакций связей движущейся механической системы……… 105 ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ СТАТИКИ…………………………… 121 Задание Д-11. Применение принципа возможных перемещений к исследованию равновесия механической системы……………………..... 121 ПРИНЦИП ДАЛАМБЕРА – ЛАГРАНЖА Задание Д-12. Применение общего уравнения динамики к исследованию движения механической системы с одной степенью свободы……….... 132 МЕТОД ОБОБЩЕННЫХ КООРДИНАТ И УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА……………… 146 Задание Д-13. Исследование равновесия механической системы методом обобщенных координат…. 146 Задание Д-14. Применение метода обобщенных координат к исследованию движения механической системы с одной степенью свободы………………………………………… 149
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ………...……………….. 154
|
радиус инерции барабана 2 относительно неподвижной оси вращения 
; 
Определить величины ускорений 
груза 1 и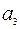 
центра масс катка 3 (рис. 68, а).
груза 1 (рис. 68, б).
, (1)
. (2)
, (3)
− момент инерции барабана относительно его оси вращения;
− момент инерции катка относительно центральной оси, перпендикулярной его плоскост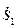и.
.
и 
в уравнение ( 
), а также учитывая, что
, получим:
.
;
, поскольку кинетическая энергия рассматриваемой системы от выбранной обобщенной координаты не зависит;
.
барабана 2 , силу тяжести 
катка 3, а также учтем силу трения скольжения 
как реакцию неидеальной связи, условно переведенную в разряд активных сил. Реакции идеальных связей системы на схеме не указываются и в расчет не вводятся.
получит положительное приращение 
. Тогда
, (4)
−сумма элементарных работ активных сил на соответствующих возможных перемещениях их точек приложения:
;
− вариация выбранной обобщенной координаты.
центра масс катка выражается через возможное перемещение 
через скорость 
груза, т. е.
и 
.
.
; 
,
м/с2; 
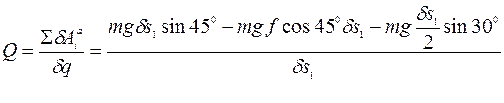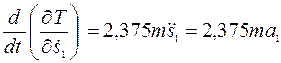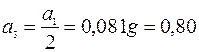м/с2.
м/с2; 
м/с2.