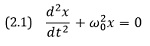ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Лекция вторая. Моделирование — универсальный инструмент синергетики (или что общего у груза на пружинке с зайцами и лисами)
Понятие модели.Модель — нечто похожее по своим свойствам на оригинал, создаваемое и (или) используемое человеком для реализации своих целей. Выбор той или иной модели определяется целью моделирования. Познавательная роль моделей.Модели играют роль «фотоаппаратов», «очков», «фильтров», через которые мы рассматриваем мир. Хорошей аналогией активной познавательной роли модели является фонарь, освещающий некоторую область в окружающей тьме. Какие бывают модели и как они рождаются.По своему происхождению модели можно условно разделить на 4 группы: 1) полученные интуитивно — из головы, например, придумыванием красивых уравнений; 2) упрощением известного более общего — по принципу «от общего к частному», как деловое платье можно сконструировать из мудреного творения кутюрье, оторвав лишние рюшки и спрямив некоторые линии; 3) по принципу от частного к общему — когда берут известные простые модели и объединяют их в ансамбль; 4) непосредственно из данных эксперимента, наблюдения. Модели могут иметь вид предметов, рисунков, формул, мыслимых образов. Мы ограничим рассмотрение лишь моделями, отражающими естественно-научное знание, а они, как правило, формулируются на языке математики. Но существуют и примеры изложения основ синергетики без формул, например, книга Н.Н. Моисеева Расставание с простотой. Особая роль математических моделей.Математика — наука о количественных отношениях и пространственных формах действительного мира. Сначала она появилась как набор полезных правил и формул для решения практических задач, с которыми люди сталкивались в повседневной жизни. Ее создали цивилизации Древнего Египта и Вавилона около 3 тысячелетий до н. э. Но только приблизительно в VI веке до н.э. древние греки уловили возможность использования математики в качестве инструмента для получения новых знаний (подробнее см. Стивен Строгац. Удовольствие от х). Математика как логический вывод и средство познания природы появилась в связи с тем, что к VI веку сложилось миропонимание, сводящееся к следующему: природа построена рационально, а явления протекают по точному плану, который в конечном итоге является математическим, человеческий разум всесилен, а поэтому этот план можно раскрыть и познать. В результате подобных наблюдений родились два основополагающих принципа: · природа устроена на математических принципах; · числовые соотношения — основа, единая сущность и инструмент познания порядка в природе. В чем причина исключительной эффективности математики?Над этим задумывалось большое число мыслителей от древности до наших дней. По ответам их можно условно разделить на 2 группы. Первые считают, что математики подбирают аксиомы так, чтобы выводимые из них следствия согласовались с опытом, т. е. математика подстраивается под природу. Другими словами, всеобщие и необходимые законы опыта принадлежат не самой природе, а только разуму, который вкладывает их в природу. Вторые считают, что мир основан на математических принципах. Что общего находит синергетика в системах различной природы?Например, колебания грузика на пружине, концентрации молекул в химической реакции или численность популяции одного биологического вида в условиях его конкуренции с другим видом при определенных условиях описывает одно и то же уравнение осциллятора:
Для всех перечисленных объектов и математической модели общим является повторяющийся через период Т = 2π/ω0 вид зависимости величины x от времени. Более того, можно указать даже форму колебаний, которая описывается функциями синуса или косинуса. Обогатившись математическим моделями, созданными исследователями различных природных и искусственных объектов и проанализированных поколениями математиков и естественников, синергетика рассматривает процессы самоорганизации — образования пространственных неоднородностей (структур) в системах, состоящих из большого числа элементов и их эволюции во времени. |