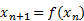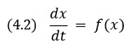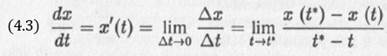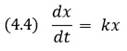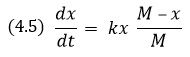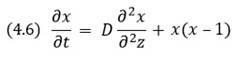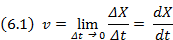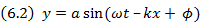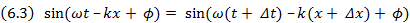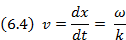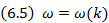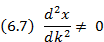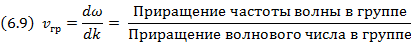ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Лекция четвертая. Динамическая система

Предыдущая 1 2 345 6 7 8 Следующая

Что такое «динамическая система»?Динамическая система является моделью какой-либо реальной физической, химической, биологической, социальной или любой другой системы. Для того чтобы определить динамическую систему, необходимо:

1. Задать набор величин (переменных), однозначно характеризующих состояние системы.

2. Задать правило (оператор эволюции), по которому, зная текущее состояние системы, можно определить (предсказать) ее состояние в следующий момент времени.

Динамические системы являются видом математических моделей, отражающих мировоззренческий принцип детерминизма.

С понятием «динамическая система» тесно связаны понятия «фазовое пространство». Например, предположим, что нужно рассмотреть эволюцию системы домашняя кошка. В качестве переменных величин, характеризующих эту систему, выберем рост кошки и вес кошки. Сначала, будучи котенком, кошка имеет небольшой рост и вес (см. точку 0 на рис. 4.1). Затем, по мере взросления, рост и вес кошки увеличиваются (точки 1–4), и кошка достигает «расцвета сил» (точка 5). После этого рост кошки уже не изменяется, а вес уменьшается (точки 6–9).

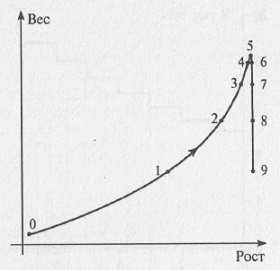
Рис. 4.1. Зависимость роста и веса кошки от времени

Этот же самый процесс можно изобразить по-другому: отложить по одной оси рост, а по другой — вес кошки (рис. 4.2). Тогда каждая точка на плоскости (рост; вес) будет однозначно характеризовать состояние системы «домашняя кошка». Верно и обратное — каждое состояние рассматриваемой системы можно представить точкой на этой плоскости. Таким образом, имеет место взаимно однозначное соответствие между состоянием, в котором находится кошка, и точкой на плоскости (рост; вес). Такая плоскость, по осям координат которой откладываются переменные величины, характеризующие состояние системы, называется фазовой плоскостью. Если бы переменных величин, характеризующих состояние системы, было бы не две, а больше (скажем, три), то речь шла бы не о фазовом пространстве.

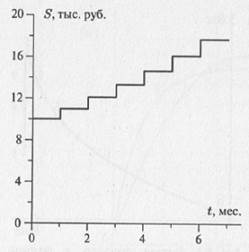
Рис. 4.2. Фазовая плоскость с фазовой траекторией для динамической системы домашняя кошка

Сначала, когда кошка является маленьким котенком, ее рост и вес невелики (точка 0 на рис. 4.1). На фазовой плоскости изображающая точка находится в этот момент времени около начала координат (точка 0 на рис. 4.2). Затем, когда кошка взрослеет, изображающая точка двигается по фазовой плоскости в сторону больших значений роста и веса (точки 2–5, рис. 4.2). Когда кошка начинает стареть, ее рост практически не изменяется, а вот вес уменьшается, поэтому изображающая точка двигается по фазовой плоскости так, что ее координата «рост» остается постоянной, а координата «вес» неуклонно уменьшается (точки 5–9, рис. 4.2). Линия, по которой двигается изображающая точка, называется фазовой траекторией. Таким образом, фазовая траектория характеризует эволюцию системы с течением времени, каждая точка фазовой траектории соответствует определенному состоянию системы в тот или иной момент времени. И если на графиках зависимости переменных, характеризующих состояние системы от времени, течение времени проявляется в том, что нужно рассматривать все большее значение по оси абсцисс (по горизонтальной оси), то на фазовой плоскости ход времени проявляется в движении изображающей точки по фазовой плоскости.

Среди динамических систем можно выделить два больших класса: динамические системы с дискретным и непрерывным временем.

Динамические системы с дискретным временем.Иногда достаточно знать состояние системы не в каждый момент времени, а только в некоторые определенные моменты времени. Например, вы положили в банк 10 тыс. руб. под 10% в месяц. Тогда, через месяц у вас на счету будет 11 тыс. руб., через 2 месяца — 12 100 руб. и т.д. В течение месяца сумма не изменяется. Следовательно, нет необходимости указывать сумму в каждый момент времени. Достаточно знать сумму на начало каждого месяца. Зависимость суммы вашего вклада S от времени t будет иметь вид, приведенный на рис. 4.3. Иными словами, для того, чтобы описать систему «счет в банке», необходимо указать сумму вклада лишь в определенные моменты времени. В этом случае время t не изменяется непрерывно, а принимает конечный набор значений t = 1 месяц, 2 месяца и т.д. Говорят, что время t принимает дискретный набор значений, оно (время) является дискретным. Системы, для описания которых используется переменная времени, принимающая дискретный набор значений, называются системами с дискретным временем.

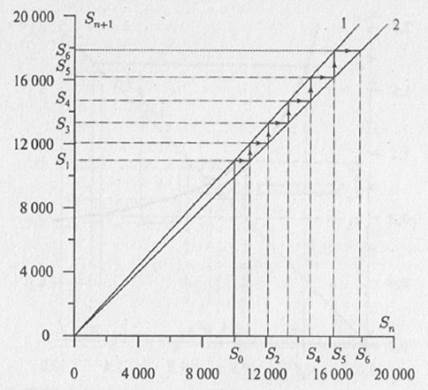
Рис. 4.3. Зависимость суммы вклада от времени

Можно записать, что

(4.1)

где х_n+1 — переменная величина, характеризующая состояние системы в n-й момент дискретного времени, f(x) — некоторая функция (оператор эволюции), которая позволяет по известному состоянию системы в n-й момент дискретного времени однозначно определить (предсказать) ее состояние в следующий (n + 1)-й момент дискретного времени.

Существует еще один способ графического представления того, как ведет себя переменная S. Для этого нужно отложить не зависимость суммы S от времени t, а зависимость суммы вклада в (n + 1)-й момент дискретного времени S_n+1 от суммы вклада в предыдущий n-й момент дискретного времени S_n. Фактически, нужно построить график функции f(S). Поведение системы с дискретным временем приведено на рис. 4.4.

Рис. 4.4. Диаграмма Ламерея для задачи о банковском счете: 1 – S_n+1 = f(S_n); 2 – S_n+1 = S_n (прямая, идущая под углом 45%)

Динамические системы с непрерывным временем.Такие динамические системы часто называют потоковыми системами. В этом случае значение переменной времени изменяется непрерывно, и в любой момент времени можно определить значения переменных величин, характеризующих динамическую систему. Для динамических систем с непрерывным временем оператором эволюции служат обыкновенные дифференциальные уравнения:

х — единственная переменная, которая характеризует рассматриваемую динамическую систему. Эта переменная изменяется с течением времени — в таких случаях говорят, что она зависит от времени t (t — независимая переменная), или что она является функцией времени x = x(t). Как быстро изменяется с течением времени переменная x, характеризуется производной:

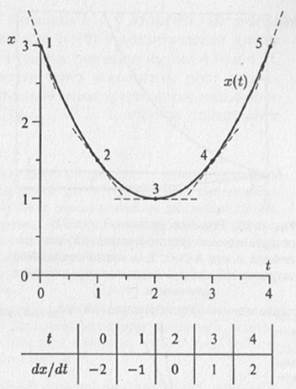
Если переменная x увеличивается с течением времени, то значение производной x'(t) является положительным, если x уменьшается с течением времени — производная оказывается отрицательной. Чем быстрее изменяется переменная x с течением времени, тем больше по модулю оказывается значение производной.

На рис. 4.5 представлена зависимость величины x, характеризующей состояние системы, от времени t.

Рис. 4.5. Зависимость переменной x от времени имеет вид: x(t) = (t – 2)²/2 + 1. В различные моменты времени t производная принимает различные значения

Дифференциальное уравнение «устроено» следующим образом: в него входят производные, а также переменные величины. Дифференциальное уравнение показывает, как связаны производные и их величины между собой. Простейшим дифференциальным уравнением является уравнение вида:

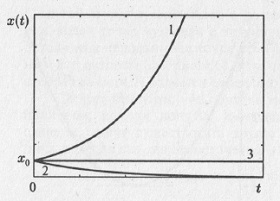
Если величина k в этом уравнении (являющаяся параметром системы) положительная, то, чем больше величина x, тем больше производная x'(t), и тем быстрее растет сама величина x(t) с течением времени t. В этом случае переменная x(t) неограниченно возрастает. В том случае, если параметр k отрицателен, величина x будет с течением времени уменьшаться и стремиться к нулю. И лишь в том случае, когда параметр k точно равен нулю, величина x не будет меняться с течением времени. Но малые «шевеления» параметра k приведут систему либо к состоянию неограниченного роста, либо к асимптотическому уменьшению величины x до нуля. Говорят, что ситуация k = 0 является вырожденной. Решение уравнения (4.4) в аналитической форме записи имеет вид
x(t) = x₀e^kx, а его график приведен на рис. 4.6.

Рис. 4.6. Решение уравнения (4.4): 1– неограниченный (экспоненциальный) рост величины x при k > 0; 2 – экспоненциальное затухание (k < 0); 3 – постоянное значение величины x (k = 0).

Любопытно, что к уравнению вида (4.4) приводят размышления, которые в 1798 году Томас Мальтус применил при описании роста численности народонаселения Земли. В этом случае x рассматривается как число людей, проживающих на Земле, t — время. Мальтус, использовавший уравнение (4.4) применительно к человеческому сообществу, пришел к выводу, что рост численности человеческого общества опережает темпы роста продовольственных запасов, а, следовательно, неизбежна жестокая конкуренция среди людей «за место под солнцем».

В реальной жизни никакая биологическая популяция не может расти неограниченно — экологическая система стабилизируется посредством ограничения природных ресурсов. Именно поэтому в 1838 году Ферхюльст предложил логистическую модель, которая более достоверно, нежели модель Мальтуса (4.4), описывает динамику популяций. Ферхюльст предположил, что ресурсы, необходимые для жизнедеятельности особей популяции, ограничены, и на рассматриваемом ареале могут одновременно проживать не более М особей. Величина М не зависит от времени и является параметром модели, который называется емкостью среды. Тогда коэффициент, отвечающий за скорость изменения численности популяции, должен зависеть от числа особей популяции x, причем при малых значениях x, когда численность популяции много меньше емкости среды (x ≪ М), ограниченность природных ресурсов не будет заметна, а значит и уравнение, и его решение должны очень мало отличаться от уравнения (4.4) и его решения. Следовательно, при малых x скорость изменения популяции должна быть близка к kх. С другой стороны, с увеличением численности популяции начинает сказываться ограниченность природных ресурсов, и коэффициент, ответственный за темп прироста популяции, должен уменьшаться, достигая нулевого значения при x = М. Уравнение, учитывающее все вышеизложенное, называется уравнением Ферхюльста (часто это уравнение также называют логистическим) и имеет вид:

Изначально, когда численность популяции мала (x ≪ М), уравнение (4.5) совпадает с (4.4), и численность популяции нарастает экспоненциально. Но по мере увеличения x начинает сказываться ограниченность природных ресурсов, скорость роста численности популяции уменьшается, и при t g ∞ численность популяции x стремится к М, а скорость роста популяции — к нулю (рис. 4.7).

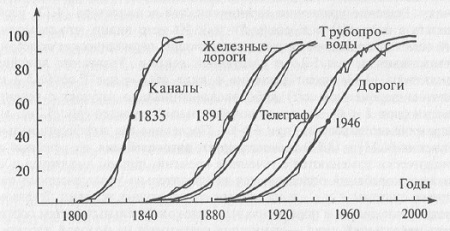
Рис. 4.7. Решение логистического уравнения (уравнения Ферхюльста): 1 – экспоненциальное приближение при x ≪ М; 2 – решение логистического уравнения

Следует отметить, что уравнение Ферхюльста достаточно хорошо описывает динамику простых биологических систем типа колонии бактерий. Не менее хорошо ложатся на логистические кривые и данные, описывающие динамику развития сетей транспорта и коммуникаций в США (рис. 4.8).

Рис. 4.8. Динамика развития инфраструктуры США

Для линейных систем выполняется принцип суперпозиции. Это означает, что если, скажем, дифференциальное уравнение (4.7) является линейным (т.е. функция f(x), стоящая в его правой части, линейна), и х₁(t), х₂(t) – решения этого уравнения, то выражение a₁х₁(t) + a₂х₂(t), где a₁, a₂ — константы — также является решением этого уравнения. Поэтому, зная некоторый конечный набор решений, можно из них получить все множество возможных решений дифференциального уравнения (или системы дифференциальных уравнений), описывающего линейную систему. Для нелинейных систем принцип суперпозиции не выполняется.

Распределенные системы.До сих пор рассматриваемые динамические системы характеризовались переменной величиной х, зависящей только от времени (их называют сосредоточенными системами). Часто системы характеризуются не только временной, но и пространственной динамикой. В этом случае поведение систем будет характеризоваться некоторой величиной (или даже набором величин), зависящей не только от времени t, но и от пространственных координат. В простейшем случае поведение системы может зависеть только от одной пространственной координаты: х = x(t, z). Подобные системы, для описания которых необходима информация не только об их изменении с течением времени, но и о пространственной динамике, называются распределенными (иногда говорят о системах с распределенными параметрами).

Одна и та же система может (в зависимости от того, какие ставятся задачи) рассматриваться и как распределенная, и как сосредоточенная. В том случае, например, когда изучается вопрос о том, как изменяется численность населения Земли с течением времени, и исследователей не интересует, как это население расселено по государствам и материкам, система «население Земли» является системой со сосредоточенными параметрами. Если же основной интерес представляет плотность расселения людей и то, как она изменялась с течением времени, то система «население Земли» будет рассматриваться как система с распределенными параметрами.

Распределенные системы описываются дифференциальными уравнениями в частных производных. Частная производная обозначается ∂x/∂t, (символ ∂ говорит о том, что производная частная) и обозначает, что вычисляется производная от функции нескольких переменных x(t,z) по переменной t. Эта частная производная характеризует, как быстро изменяется величина х с течением времени в точке с координатой z. Если бы вычислялась производная по переменной z, то она характеризовала бы, как быстро меняется величина х вдоль пространственной координаты z в фиксированный момент времени t, и обозначалась бы ∂x/∂z.

Уравнения в частных производных часто используются синергетикой. В качестве примера приведем нелинейное уравнение диффузии, являющееся эталонным:

Иногда это уравнение называют уравнением Колмогорова—Петровского—Пискунова, которые впервые рассмотрели это уравнение применительно к задаче о динамике биологической популяции, распределенной по пространственному ареалу проживания. На рис. 4.9 приведен вид решения уравнения (4.6) для различных моментов времени. Видно, что для этого уравнения характерно решение в виде бегущей волны, распространяющейся по пространству вдоль оси z.

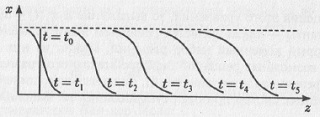
Рис. 4.9. Трансформация профиля бегущей волны плотности популяции с течением времени для нелинейного уравнения диффузии (4.6)

Лекция пятая. Колебания

Одной из задач синергетики является поиск общих закономерностей в процессах, протекающих в системах самой различной природы. Колебания — одно из таких самых общих явлений; их изучением и занимается теория колебаний. Теория колебаний устанавливает общие свойства на основе анализа некоторых эталонных математических моделей (например, гармонический, линейный, нелинейный осцилляторы), которые она конструирует и которые с завидным постоянством «обнаруживаются» везде, где есть колебания.

По определению, колебания — это изменение с течением времени какой-либо величины, обладающее той или иной степенью повторяемости.

Рассмотрим механический маятник (рис. 5.1а). Имеется подвес длиной l, закрепленный на неподвижном креплении. На подвесе закреплен груз массой m. Маятник находится в гравитационном поле Земли, ускорение свободного падения которого g. Если вывести маятник из состояния равновесия и отпустить, то он начнет совершать колебательные движения. Если трения (или, как говорят физики, диссипации) нет, то такое колебательное движение будет продолжаться вечно, причем система будет возвращаться в исходное состояние через один и тот же интервал времени. Этот интервал времени называется периодом колебаний. Он характеризует, как долго длится один цикл колебательного процесса. Здесь мы имеем дело с периодическими колебательными процессами, т.е. колебаниями, которые абсолютно точно повторяются во времени (рис. 5.1,). Максимальное отклонение положения системы от состояния равновесия называется амплитудой колебаний А. Величина амплитуды колебаний определяется величиной первоначального толчка или отклонения маятника от состояния равновесия. Если учесть наличие потерь энергии, которые всегда присутствует в реальных системах, то картина колебаний качественно изменится (рис. 5.1в): размах колебаний уменьшается с течением времени, и, в конце концов, колебания полностью прекратятся (или, как говорят физики, затухнут). Подобные колебания так и называются: затухающие колебания.

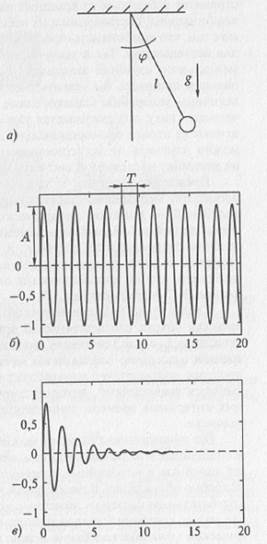
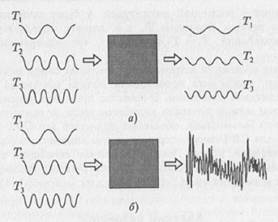
Рис. 5.1. Математический маятник: а) модель; б) вид периодических колебаний при отсутствии затуханий; в) вид затухающих колебаний

Отличительными свойствами линейных динамических систем является выполнение принципа суперпозиции и изохронность линейных колебаний. Что подразумевается под выполнением принципа суперпозиции? Давайте рассмотрим некоторую динамическую систему, о которой мы ничего не знаем, как некоторый «черный ящик» (рис. 5.2). Будем воздействовать на наш черный ящик сигналом f(t, Т₁, Т₂, ..., Т_n), в котором присутствует набор элементарных гармонических функций с различными временными масштабами Т_i.

Рис. 5.2. К пояснению принципа суперпозиции колебаний: а) линейная; б) нелинейная системы

Понаблюдаем за откликом g(t) нашего черного ящика на такой сигнал. Если в отклике будут содержаться только те же самые временные масштабы, пусть даже и с другими амплитудами, то мы имеем дело с линейной системой (рис. 5.2а). А принцип суперпозиции означает, что между разномасштабными колебательными процессами отсутствует какое-либо взаимодействие. Поэтому для линейной задачи любое решение всегда можно сконструировать из определенного набора некоторых частных решений.

Если мы имеем дело с нелинейной системой, то отклик системы будет значительно более сложным. Он будет содержать сложную совокупность частот, являющихся суммами гармоник и субгармоник частот исходного сигнала. Более того, может оказаться, что выходной сигнал будет содержать непрерывный спектр частот.

Второе важное свойство линейных колебаний — это изохронность, под которой понимается постоянство периода колебаний. Свойство изохронности означает, что независимо от того, какую энергию сообщили линейной колебательной системе, период колебаний определяется только параметрами системы и не зависит от величины этой начальной энергии. Для нелинейных систем принцип изохронности не выполняется: колебания с различной амплитудой А будут происходить принципиально с разным периодом Т, т.е. период становится функцией амплитуды колебаний: Т = Т(А). Говорят, что нелинейные колебания неизохронны.

Явление резонанса.Рассмотрим линейную колебательную систему без трения, т.е. систему, описываемую моделью гармонического осциллятора. Пусть период колебаний нашей колебательной системы Т₀. Будем воздействовать на нее внешним «негармоническим» периодическим сигналом f(t) с периодом Т (или круговой частотой ω = 2π/Т). Такую функцию можно записать в виде:

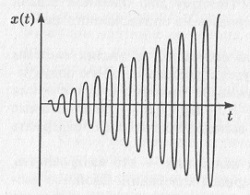
Здесь величина F_i имеет смысл амплитуды гармонической составляющей с частотой ω_i = iω (i — целое). Это так называемое разложение периодической функции в ряд Фурье. Оказывается, что если одна из частот ω_i сумме (5.1) близка к частоте собственных колебаний гармонического осциллятора (т.е. выполняется строгое условие ω_i = ω₀, либо более слабое условие ω_i g ω₀), то гармонический осциллятор начинает демонстрировать непериодические движения. Амплитуда колебаний растет со временем; темп этого нарастания зависит от величины амплитуды внешнего воздействия F_i (рис. 5.3). Это явление носит название резонанса. Физический энциклопедический словарь определяет явление резонанса как «резкое возрастание амплитуды установившихся вынужденных колебаний, которое имеет место при приближении частоты внешнего гармонического воздействия к частоте одного из собственных колебаний данной колебательной системы».

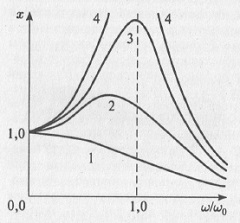
Рис. 5.3. Рост амплитуды колебаний гармонического осциллятора при явлении резонанса

Видно, что мы столкнулись с типичным проявлением неустойчивости, когда слабому внешнему возмущению соответствует на больших временах катастрофический размах амплитуды колебаний. Наша модель гармонического осциллятора «вышла из подчинения» и стала неверной. Неустойчивость — результат идеализации исходной системы. «Всякая идеализация, — по выражению Л. И. Мандельштама, — обладает способностью мстить за себя, обладает способностью создавать внутренние затруднения». Действительно, идеальная модель должна быть исправлена либо за счет диссипативных процессов (при этом она может остаться линейной), либо в ней должны быть учтены нелинейные эффекты.

При учете потерь в установившемся режиме в линейной колебательной системе имеют место незатухающие синусоидальные колебания с периодом внешней силы. Зависимость амплитуды таких колебаний от частоты вынуждающей гармонической силы носит название резонансной кривой (рис. 5.4). Из рисунка видно, что амплитуда колебаний максимальна, когда частота вынуждающей силы близка к частоте собственных колебаний, но не точно равна ей. Чем меньше потери, тем «острее» резонансная кривая. При отсутствии потерь амплитуда линейных колебаний уходит в бесконечность, и мы получаем «нефизический» результат.

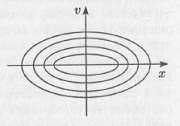
Рис. 5.4. Резонансные кривые линейного осциллятора: кривые 1-3 соответствуют случаям со все уменьшающимися потерями; кривая 4 — потери равны нулю

Другой способ «подчинить модель» — учесть нелинейность. Действительно, при резонансе имеет место рост размаха колебаний, а линейные колебания, как мы уже обсуждали выше, — это колебания с малой амплитудой. Поэтому в какой-то момент при резонансе линейные модели должны «перестать работать», и необходим учет нелинейных эффектов, например, уже обсуждаемой выше зависимости собственной частоты колебаний от их амплитуды — неизохронности колебаний.

Нелинейные колебания.Наш мир так или иначе нелинеен, это мир нелинейных систем. Свойства нелинейных систем зависят от их состояния. Математическое поведение нелинейных систем описывается нелинейными уравнениями, содержащими изучаемые величины в степенях больше единицы или коэффициенты, зависящие от этих величин. Э.Петерс в своей книге Хаос и порядок на рынках капитала пишет: «Когда я был аспирантом-математиком, то мы изучали только линейные уравнения. Мы изучали их потому, что они имеют единственное решение. Они имели приложения в физике и технике. Они были аккуратны. Нелинейные дифференциальные уравнения выглядели бесполезными ввиду того, что имели множество решений, которые казались не относящимися к реальности. Они были сложны, беспорядочны и выглядели исключениями. Теперь мы знаем, что... эти уравнения полезны именно по тем причинам, по которым их стремились избегать раньше. Жизнь неупорядоченна. Она изобилует возможностями. Поэтому необходимы модели со множеством возможных решений» (см. также Эдгар Петерс. Фрактальный анализ финансовых рынков).

По И. В. Пригожину — одному из создателей науки о сложном — в дифференциальном уравнении, описывающем эволюцию нелинейной системы, меняется некоторый управляющий параметр. При определенном значении параметра возникают, по крайней мере, два пути эволюции системы. Говорят, что имеет место бифуркация (см. Илья Пригожин. Порядок из хаоса).

Ю.А. Данилов: «В физике нелинейность — это учет различного рода взаимодействий, обратных влияний и тонких эффектов, ускользающих от более грубых сетей линейной теории. В химии нелинейность отражает обратные связи в сокровеннейших механизмах реакций. В биологии нелинейность исполнена высокого эволюционного смысла: только сильная нелинейность позволяет биологическим системам «...услышать шорох подползающей змеи и не ослепнуть при вспышке близкой молнии. Те биологические системы, которые не смогли охватить диапазон жизненно значимых воздействий среды, попросту вымерли, не выдержав борьбы за существование. На их могилах можно было бы написать: „Они были слишком линейными для этого мира"».

В социальных и экономических системах нелинейность тоже проявляется в виде взаимодействия. Однако нелинейность таких систем очень сильно определяется психологией как отдельного индивидуума, так и социальных групп. Здесь интересно проследить крушение линейной парадигмы для описания процессов на финансовых рынках. До недавнего времени все подобные модели были линейны и базировались на двух основных предположениях.

• Модель рационального инвестора. Она предполагает, что инвесторы линейно реагируют на информацию, т. е. используют ее сразу после получения, а не ожидают ее накопления в ряде последующих событий. Это означает, что прошлая информация всегда учтена, найдя свое отражение в стоимости ценных бумаг на данный момент. С точки зрения математики это означает, что рациональный инвестор желает среднестатистической эффективности. Он оценивает потенциальную прибыль методом вероятностного взвешивания, который дает ожидаемую прибыль. Риск измеряется как стандартное отклонение прибылей. Инвесторы предпочитают стратегию, которые дают наивысшую прибыль при заданном уровне риска. Они не любят рисковать.

• Модель эффективного рынка. Цены отражают всю имеющуюся на данный момент информацию. Изменения в цене не соотносятся между собой. Стоимость определяется консенсусом большого количества участников рынка.

Оба этих предположения означают, что модели финансового рынка строятся на основе линейного подхода к обществу. Если следовать ему, то люди, получая информацию, немедленно ее используют. Можно показать, что в рамках линейной теории прибыли нормально распределены и приблизительно независимы. Однако доводы, лежащие в основе линейной модели рынка капитала, несостоятельны. Линейная модель должна быть заменена нелинейной. Где же в этой модели возникают нелинейные эффекты? Они в первую очередь лежат в психологии человека.

• Люди не реагируют на информацию сразу после ее получения. Они откликаются на нее некоторое время спустя, если она подтверждает изменение в недавнем тренде. Эта нелинейная реакция — противоположность линейной реакции гипотетического рационального инвестора.

• В психологии нет подтверждений тому, что люди являются более рациональными в совокупности, чем поодиночке. Доказательством этому служат социальные перевороты, преходящие увлечения и моды.

• Люди не всегда питают отвращение к риску и часто стремятся рисковать. Особенно если осознают, что они обречены на потери, если не будут этого делать (люди более склонны к риску ради избежания потерь, чем ради получения выгод; см. Даниэль Канеман. Думай медленно… решай быстро).

• Люди полны предубеждений в своих субъективных оценках. Так они уверены в своих предсказаниях всегда существенно больше, чем это оправдано имеющейся информацией.

Представление колебаний в фазовом пространстве.Эволюция динамических систем наблюдается в пространстве состояний системы или, как его еще называют, фазовом пространстве. Можно сказать, что фазовое пространство — это некоторое абстрактное пространство, по осям которого отложены переменные нашей системы. Поэтому, если нам известны все переменные системы, то графически обозреть динамику системы не представляет сложности. Мы просто наносим переменные на координатную плоскость. Если переменных всего две, то одну из них принимаем за х, другую — за у и вычерчиваем зависимость в декартовых координатах, т.е. наносим величину одной из них относительно значения другой в один и тот же момент времени. Это называется фазовым портретом системы — он вычерчивается в фазовом пространстве. Размерность фазового пространства зависит от количества переменных, характеризующих динамику системы. Если число переменных не более трех, то такой фазовый портрет можно наблюдать визуально. В противном случае размерность фазового пространства больше трех, и для визуального наблюдения нужно строить проекции или сечения фазового пространства.

Рассмотрим вначале самые простые линейные системы. В случае гармонического осциллятора фазовое пространство двумерно. Поэтому фазовый портрет колебаний «живет» на плоскости. Рассмотрим опять наш механический маятник. Переменными в такой системе выступают скорость и положение. Их и будем откладывать по осям нашего пространства. На фазовой плоскости линейного маятника без трения (гармонического осциллятора) есть единственная особая точка — начало координат (рис. 5.5). Эта особая точка характеризует изолированное состояние равновесия гармонического осциллятора и носит название центра. Центр соответствует поведению маятника, покоящегося в состоянии равновесия. Если теперь маятнику сообщить начальную энергию («просто» толкнуть), то он начинает раскачиваться, причем при отсутствии трения его энергия не уменьшается, как не уменьшается и размах колебаний, который полностью определяется величиной начального толчка. Все фазовые траектории в данном случае — эллипсы — замкнутые кривые. Такие траектории соответствуют периодическим движениям, поскольку фазовая точка движется по замкнутой фазовой траектории и, выйдя из какой-то точки фазовой плоскости, через некоторое конечное время вернется в нее же (система имеет то же самое положение и ту же самую скорость — процесс повторяется). Причем «время возвращения», или период колебаний, является конечным. Более того, этот период не зависит от того, по какой фазовой траектории движется система, т.е. период колебаний не зависит от амплитуды малых колебаний. Об этом свойстве изохронности мы уже упоминали выше.

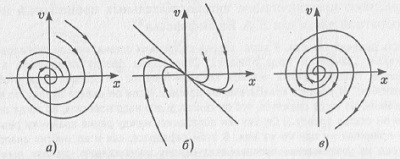
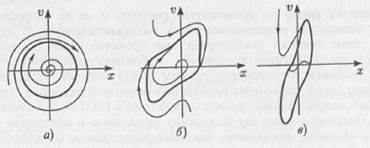
Рис. 5.5. Фазовый портрет гармонического осциллятора

Фазовый портрет меняется, если мы вводим в осциллятор диссипацию. Пусть она будет малой. В этом случае первоначально сообщенная маятнику энергия рассеивается за счет трения и амплитуда колебаний становится все меньше и меньше. Если нарисовать одну из переменных в зависимости от времени, то результирующая волнистая линия будет постепенно уменьшать свою амплитуду до нуля — кривая становится прямой линией. В фазовом пространстве (координатах положение — скорость) мы получим спиральную линию, которая выходит из какой-то точки фазового пространства (которая характеризует начальное состояние системы) и заканчивается в начале координат, когда маятник останавливается. Если мы сообщим маятнику большую начальную энергию, то колебания будут продолжаться дольше и будут обладать большей начальной амплитудой, но тем не менее временной ряд придет к нулевому значению, а фазовый портрет — в начало координат. Можно сказать, что в этом случае в фазовом пространстве система «притягивается» к началу координат: где бы ни брала свое начало система, она приходит к началу координат — своему состоянию равновесия. Такое притягивающее множество, к которому сходятся все фазовые траектории из какой-либо области фазового пространства, называется аттрактором. Такой аттрактор называется фокусом и является простейшим примером аттрактора (рис. 5.6а). В случае большой диссипации состояние маятника также эволюционирует в фазовом пространстве к началу координат (положению равновесия), но теперь уже не колебательным образом. Фазовый портрет в этом случае представлен на рис. 5.7б, а сам аттрактор называется узлом. Заметим, что фазовые траектории, по которым движется гармонический осциллятор, не являются аттракторами, так как к ним не притягиваются никакие из траекторий. Гармонический осциллятор является консервативной системой (т.е. системой без диссипации), для которой в фазовом пространстве не существует аттракторов.

Рис. 5.6. Фазовые портреты линейного осциллятора: а) устойчивый фокус; б) узел; в) неустойчивый фокус

Важно то, что и узел, и фокус являются устойчивыми состояниями равновесия, т.е. малые отклонения фазовой траектории от них (например, вызванные либо искусственно, либо спровоцированные шумами) так и остаются малыми и имеют тенденцию уменьшаться. Узел и фокус являются примерами простых аттракторов. Однако возможна ситуация, когда диссипация отрицательна (такая ситуация возможна в экономическом маятнике). В этом случае состояние равновесия становится неустойчивым (неустойчивый фокус), и все спиральные траектории уходят из него. Такое неустойчивое состояние равновесия называют репеллером (рис. 5.7в).

Автоколебания и их свойства.Возникает вопрос: возможны ли периодические колебания, образом которых в фазовом пространстве являются замкнутые линии, в системах с трением? Оказывается, да, но системы должны быть принципиально нелинейными! Диссипативные системы, которые демонстрируют незатухающие колебания, называются автоколебательными. Простейшим примером автоколебательной системы являются колебания маятника в часах.

Автоколебания являются незатухающим колебательным процессом в диссипативной системе. Они не могут существовать, если нет какого-либо источника энергии и элемента, рассеивающего энергию (если нет диссипации энергии). Причем рассеивающий элемент должен взаимодействовать с источником энергии следующим образом: при установившихся периодических колебаниях энергия потерь в точности компенсируется в течение одного периода за счет источника, т.е. автоколебательная система непрерывно переводит энергию источника в энергию потерь (если, например, энергия теряется на трение, то энергия источника непрерывно переводится в тепло).

В линейной системе автоколебаний быть не может, даже если в ней имеет место отрицательное затухание. Для автоколебаний связь между источником энергии и колебательным элементом должна быть нелинейной. В простейших автоколебательных системах (автогенераторах), как правило, можно выделить колебательную систему с затуханием, усилитель и нелинейный ограничитель — звено «обратной связи».

Важное свойство автоколебаний — независимость вида и свойств автоколебаний от начальных условий. Если взять наш механический маятник, отвести его на некий угол и отпустить, то размах колебаний (при отсутствии потерь) будет как раз равен этой величине отклонения. Если отвести маятник на угол в два раза меньший, то и размах будет в два раза меньше. То есть для «обычных» колебаний амплитуда определяется начальными условиями. Для автоколебаний дело обстоит несколько иначе: их внешний вид определяется только свойствами самой автоколебательной системы и не зависит от начального состояния. Так маятник в ходиках можно отвести в начальный момент на любой угол, однако в установившемся режиме память об этом будет потеряна: автоколебания будут происходить с одной и той же амплитудой и частотой, независящими от начальной величины отклонения маятника.

Можно ли изменить характеристики (амплитуду, частоту, форму) автоколебаний? Да, но для этого надо изменять свойства самой автоколебательной системы. В случае ходиков частота автоколебаний изменяется путем изменения длины маятника (так и поступают с ходиками, когда они «спешат» или «отстают»).

В фазовом пространстве образом периодических автоколебаний являются предельные циклы Пуанкаре. Предельный цикл — замкнутая фазовая траектория, к которой стремятся все соседние траектории (рис. 5.7). Форма предельного цикла может быть различной. Главное, что предельный цикл, в отличие от фазовых траекторий гармонического осциллятора, является аттрактором, т.е. притягивает к себе траектории из других областей фазового пространства.

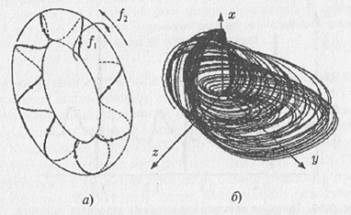
Рис. 5.7. Предельные циклы Пуанкаре в фазовом пространстве

В динамических системах автоколебания могут быть не только периодическими, но и квазипериодическими. Образом квазипериодических движений в фазовом пространстве является тор (рис. 5.8а). Он может реализоваться только в системе с фазовым пространством, размерность которого больше или равна трем. Особенностью аттрактора квазипериодических колебаний является то, что траектория нигде не замыкается, всюду плотно «наматываясь» на поверхность тора.

Рис. 5.8. Тор и странный аттрактор

Но и этим не ограничиваются возможные типы аттракторов в нелинейных системах. Последний тип аттрактора — хаотический или странный аттрактор. Он является образом хаотических автоколебаний (рис. 5.8б). Странные аттракторы — удивительные объекты. В системах, демонстрирующих хаотическую динамику, равновесие становится областью в фазовом пространстве — именно к этой области, называемой странным аттрактором, притягиваются все фазовые траектории, исходящие из других точек фазового пространства. Странные аттракторы демонстрируют фрактальные свойства своей структуры.

Примеры колебаний.В биологии классическим примером автоколебательной системы является сердце. С одной стороны, энергия, запасенная в клетках сердечной ткани, расходуется на сокращение сердечной мышцы (чтобы обеспечить перекачку крови по кровеносной системе) и на ее потребление клетками сердца для поддержания своей жизнедеятельности. С другой стороны, запас энергии пополняется при прокачке через сердце артериальной крови, богатой кислородом.

В экономической жизни автоколебания наиболее ярко иллюстрируются наличием долгосрочных циклов (с периодом 45-65 лет) периодического изменения различных экономических показателей. Такие экономические циклы связаны с именем выдающегося русского экономиста Н.Д. Кондратьева (1892–1938).

Еще один пример колебательных явлений — климатические изменения. Регулярная смена времен года, которая воспринимается нами как нечто само собой разумеющееся и привычное, — тоже колебания, как и суточные колебания температуры (днем температура выше, ночью ниже). Но речь пойдет не о столь привычных нам колебаниях, а о глобальных колебаниях, на первый взгляд незаметных, которые имеют другой временной масштаб — очень большую длительность, превышающую длительность человеческой жизни. Если на протяжении долгого времени проследить за значением средней температуры, то окажется, что эта величина также не была постоянной, а изменялась, совершая колебания, с чем связаны различные эпохи эволюционного развития нашей планеты (рис. 5.9).

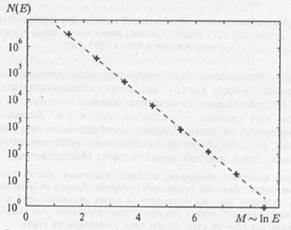
Рис. 5.9. Колебания климата

Еще один пример колебательного поведения — динамика численности биологических популяций. Одним из факторов, позволяющих объяснить колебания численности популяций, является межвидовое взаимодействие особей двух популяций: так называемых «жертв», которые питаются природными ресурсами (различные растения), и «хищников», которые в основном питаются «жертвами».

Наблюдаются колебания и в химических системах. Впервые колебательную химическую реакцию, проявляющуюся в виде периодических вспышек при окислении паров фосфора, наблюдал Роберт Бойль в конце XVII века. Современная история исследований колебательных химических реакций в жидкой фазе началась в 1951 году, когда Б.П. Белоусов открыл колебания концентрации окисленной и восстановительной форм церия в реакции взаимодействия лимонной кислоты с броматом, катализируемой ионами церия. Позже в работах И. Р. Пригожина, бельгийского физика и химика, лауреата Нобелевской премии 1977 года за работы по термодинамике необратимых процессов, было показано, что колебательные химические реакции не только возможны, но и весьма вероятны вблизи стационарного состояния, достаточно удаленного от термодинамического равновесия.

В конце 1961 года работа Б.П. Белоусова была продолжена А. М. Жаботинским, который получил колебания при использовании в качестве восстановителя в реакции Белоусова не только лимонной, но и малоновой, а также яблочной кислот. Новость об этой удивительной реакции, которая в наше время носит название реакции Белоусова—Жаботинского, очень быстро обходит весь мир и начинает интенсивно изучаться во многих странах. Именно с реакции Белоусова—Жаботинского можно говорить о признании научным сообществом возможности колебательных химических реакций.

Наконец, говоря о колебаниях, оказывающих влияние на человеческую жизнь, нельзя не сказать несколько слов о землетрясениях — колебаниях земной коры, которые длятся, как правило, очень недолго, но по своим последствиям могут быть весьма серьезными. На рис. 5.10 статистические данные о землетрясениях представлены в виде графика, на котором по оси абсцисс отложена магнитуда М землетрясения, пропорциональная логарифму энергии Е землетрясения, а по оси ординат — число землетрясений с такой магнитудой. Видно, что распределение числа землетрясений N по их энергиям описывается с высокой степенью точности степенной зависимостью вида N(E) ~ НЕ^–^b.

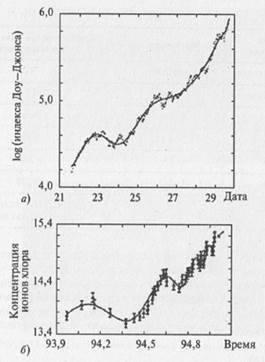
Рис. 5.10. Распределение землетрясений разной силы во всем мире (с 1990 года), происходящих в среднем за год

Таким образом, следует сделать вывод о том, что колебания оказываются явлением, часто встречающимся в системах самой различной природы. Понятно, что разные системы изучаются разными науками: социальные системы исследуются историей, экономикой, социологией, политологией и т.д., механические или, например, электрические — механикой и физикой, земная кора — геологией, численность популяций — биологией, колебательные химические реакции — химией, изменения температуры или климата — метеорологией и т.п. Теория колебаний пытается взглянуть на разнообразные колебательные явления с единой точки зрения, выявить общие закономерности, свойственные колебательным системам.

В качестве подтверждения общности явлений в системах различной природы рассмотрим два графика (рис. 5.11), взятые из статьи Г. Г. Малинецкого Хаос. Тупики, парадоксы, надежды. На первом приведена зависимость индекса Доу-Джонса от времени перед Великой депрессией в США, а на втором — зависимость концентрации газа от времени перед землетрясением. Безусловно, эти две системы (человеческое общество и земная кора) совершенно различны, но, по всей видимости, существуют общие универсальные закономерности, обуславливающие одинаковый вид двух различных кривых перед событиями, качественно меняющими состояние систем. Синергетика стремится выявить подобные общие закономерности, возникающие в разных системах, и описывать их на своем языке, близком к языку математики.

Рис. 5.11. Колебания: а) логарифма индекса Доу-Джонса от времени перед Великой депрессией 1929 года; б) концентрации ионов хлора в родниках перед землетрясением в Кобе в 1995 году

Лекция шестая. Волны

Что такое волна?Волной называется явление распространения колебаний в пространстве. Физический энциклопедический словарь: волны — возмущения, распространяющиеся с конечной скоростью в пространстве и несущие с собой энергию... без переноса вещества (хотя последний может иметь место как побочное явление). Самое главное в этом определении то, что волны переносят энергию без переноса вещества.

Более общее определение понятия волны может прийти из рассмотрения нефизических ситуаций. Вот одна из страниц русской истории — 25 апреля 1742 года. В этот день состоялась коронация императрицы Елизаветы, дочери Петра I, на русский престол. Будущая императрица пожелала, чтобы момент возложения патриархом короны на ее голову был отмечен в новой столице России — Петербурге — выстрелом пушки Петропавловской крепости. Но по тогдашним законам коронация русских царей происходила в Москве в Успенском соборе. Радио и телевидения не было... Но способ реализации желания Елизаветы нашли. На всем примерно шестьсот пятидесяти километровом пути от собора в Москве до крепости в Петербурге на расстоянии прямой видимости (примерно сто метров) друг от друга выстроили солдат. Понадобилось приблизительно шесть тысяч пятьсот человек; в руке у каждого был флажок. В момент, когда корона коснулась головы Елизаветы, первый солдат взмахнул флажком, следующий повторил его действия, затем последовательно все остальные. Минут через десять-двадцать известие о коронации дошло до артиллериста в Петропавловской крепости, поскольку время реакции человека составляет десятые доли секунды. Спрашивается: что же переместилось из Москвы в Петербург?

Любой из солдат стоял на своем месте; правда, каждый взмахнул флажком. На языке науки действия солдата (поднял и опустил руку с флажком) означает изменение его состояния, или фазы. Именно это изменение состояния (фаза) и перемещалось вдоль цепи солдат. Тогда можно дать следующее весьма общее определение волны.

Перемещение в пространстве изменения состояния (фазы) называется волной.

Свойства волн.

1. Перенос энергии. Волны, как и всякий движущийся объект, переносят энергию в процессе всего распространения.

2. Волна обладает импульсом. Подобно движущимся частицам, волны обладают импульсом.

3. Скорость волны. Поскольку волна распространяется в пространстве от одной точки к другой, то она обладает скоростью. В физике скорость характеризует быстроту изменения наблюдаемой величины и определяется отношением изменения этой величины к длительности отрезка времени, за которое это изменение произошло. Так, если речь идет о скорости движения точки вдоль некоторой оси координат X, изменение координаты ΔХ делят на время Δt и, устремляя величину Δt к нулю, находят скорость точки.

Но при рассмотрении волн не все так просто. Давайте рассмотрим фотографию волн от капли, упавшей в воду (рис. 6.1). От капли, возмущающей только очень малую область поверхности воды, начинают расходиться круги, а в центре быстро расширяющейся системы кругов образуется область спокойной воды. Для анализа этой сложной картины невозможно обойтись без рассмотрения волны, которой в чистом виде нет в природе. Это — бесконечная гармоническая волна, описываемая формулой:

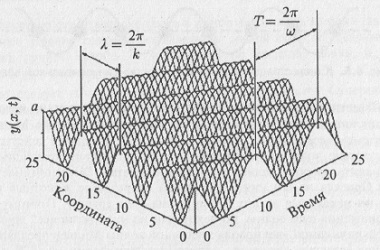
где у — величина возмущения, распространяющегося в пространстве (для волны на поверхности воды – это отклонение точки поверхности по вертикали, для электромагнитной волны — интенсивность электрического или магнитного полей, для волны эпидемии — число заболевших и т.д.); а — постоянная амплитуда волны; (ωt – kx+ ϕ) – фаза волны; ω — постоянная частота (ω = 2π/Т, Т — период волны); k = 2π/λ — постоянное волновое число (λ — длина волны); ϕ — начальная фаза (рис. 6.2).

Рис. 6.1. Волны, расходящиеся от капли, упавшей на поверхность жидкости

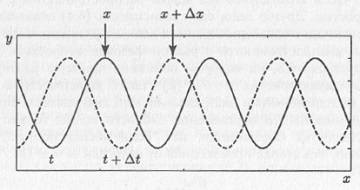
Рис. 6.2. Изображение формы синусоидальной (гармонической) волны в пространстве «время — координата — размах колебаний». На рисунке показаны такие важные характеристики волны, как временной период (период колебаний Т), пространственный период (длина волны λ), амплитуда волны

Следуя физическому определению скорости (6.1), проведем следующие простые рассуждения. Пусть мы наблюдаем за распространением гармонической волны как на рис. 6.3, на котором показан профиль волны в два момента времени, разделенных интервалом Δt. Как видно из рисунка, волна распространяется вправо так, что за время Δt она прошла путь Δx. Начало и конец этого пути отмечен на рис. 6.3. стрелками (для удобства мы следили за распространением максимума волны). По аналогии с формулой (6.1) под скоростью волны можно понимать величину v = Δx/Δt.

Рис. 6.3. К введению фазовой скорости волны

Из рис. 6.3 следует, что значения функции у, описывающей профиль волны, одинаковы в начале и конце пути, следовательно, с учетом формулы (6.2) можно записать:

Последнее означает, что когда нас интересует скорость гармонической волны, то нас интересует выполнение условия постоянства фазы волны: wt – kx + ϕ = const. Дифференцируя в соответствии с определением (6.1) это выражение по времени, находим выражение для скорости гармонической волны:

Cкоростm волны (6.3) называется также фазовой скоростью v_ф.

Будут ли волны с разными частотами ω (разными длинами волн λ) распространяться с одной скоростью v_ф? Оказывается, что в зависимости от положительного или отрицательного ответа на данный вопрос мы имеем дело либо с отсутствием, либо, наоборот, с наличием дисперсии в среде, в которой распространяется волна. Дисперсию волн характеризует соотношение между частотой и волновым числом волны:

которое в теории волн принято называть дисперсионным уравнением. Если дисперсионное уравнение линейно, т.е. имеет вид:

(ω₀ есть некоторая константа), то говорят об отсутствии дисперсии в среде. Очевидно, что в этом случае все волны распространяются с одной фазовой скоростью. Другое дело, если зависимость (6.5) нелинейная. Тогда говорят о наличии в среде дисперсии, и волны с разными частотами (длинами волн) распространяются с разной фазовой скоростью.

Определение скорости волны не ограничивается понятием фазовой скорости. Если дисперсионное уравнение волны таково, что вторая производная от функции ω = ω(k):

то вводят новую характеристику волнового движения, которую называют групповой скоростью:

Каков физический смысл понятия групповой скорости? Для ответа на этот вопрос рассмотрим суперпозицию двух гармонических волн со слабо отличающимися частотами и волновыми числами, но одинаковой амплитуды. График суммарной волны у, возникшей в результате сложения двух гармонических волн, показан на рис. 6.4. Из него видно, что результатом биений двух волн оказывается ряд периодически повторяющихся групп, причем такое повторение проявляется как во времени, так и по пространству. Каждая такая группа состоит из нескольких волн.

Рис. 6.4. Графическая интерпретация возникновения групп (биений) при сложении двух гармонических волн

Групповая скорость

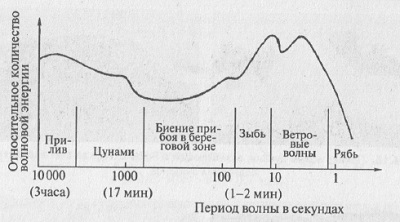
Напомним, что фазовая скорость волны есть величина v_ф = ω/k. Поскольку и v_ф и v_гр зависят от k, то понятно, что в случае, когда d²ω/dk² ≠ 0, групповая скорость отличается от фазовой. При этом волны с различной длиной волны распространяются с различными групповыми скоростями. Как влияет дисперсия в системе на распространение возмущения, представляющего собой суперпозицию (сумму) ряда гармонических волн различной длины (волновой пакет)? Поскольку компоненты возмущения с различными волновыми числами (различными длинами волн) распространяются с различными скоростями, начальное возмущение через некоторое время растянется на некоторый пространственный интервал, который будет расти со временем. В этом случае мы имеем дело с диспергирующей волной. Если d²ω/dk² = 0, то волна не диспергирующая и v_ф = v_гр. В последнем случае при распространении волнового пакета искажение не наблюдается за счет того, что все волны, составляющие пакет, распространяются с одной скоростью.

Волны на воде.Океанские волны разделяют по их периоду.

Приливные волны, образование которых связано с притяжением Луны и Солнца, — самые длинные; их длина (теоретически) составляла бы половину окружности земного шара, если бы не мешали материки, а период этих волн от двенадцати до двадцати четырех часов. В открытом море это — линейные волны из-за большой длины, а нелинейность проявляется лишь у берега.

Цунами (рис. 6.5) — волны подводных землетрясений или извержений вулканов с периодом от десяти минут до часа. В открытом море цунами — линейная волна, но в береговой зоне высота волны возрастает иногда до десятков метров.

Бор (рис. 6.6) образуется при вхождении прилива в устье реки или пролив; передний склон волны представляет собой резкий перепад высотой до нескольких метров.

Ветровые волны – наиболее характерный тип движения на поверхности моря. В них выделяют зыбь с периодом 6–16 с, волнение с периодом 5–12 с и мелкие ветровые волны с периодом 1–4 с.

Наконец, капиллярные волны — рябь — имеют в воде длину, меньшую 1,7 см. На рис. 6.7 приведен спектр реального морского волнения.

Рис. 6.5. Пример волны цунами, возникающей в Тихом океане за счет извержения подводных вулканов

Рис. 6.6. Когда сильный прилив проходит много километров по мелководью, фронт приливной волны становится все круче. Он может образовывать бору, т.е. подвижную форму гидравлического прыжка. На левом рисунке показана бора на реке Цяньтан. На правом рисунке показана волновая бора на Амазонке.

Рис. 6.7. Спектр реального морского волнения

Океанологические эксперименты последних лет показали, что течений, которые рисуют на картах в виде широких рек, в действительности не существует. Основная кинетическая энергия океана сосредоточена в громадных медленно передвигающихся океанических вихрях, подобных циклонам и антициклонам в атмосфере. Правда, если усреднить все движения вихрей за много месяцев, то получится нечто вроде известных всем океанических течений.

Нелинейные волны.Выше мы рассматривали преимущественно линейные волны. Однако, как существуют нелинейные колебания, так существуют и нелинейные волны, поведение которых описывается нелинейными уравнениями. Мир нелинейных волн богат и разнообразен. Но и в нем есть свои эталонные модели, подобные эталонным моделям теории колебаний. Среди них — простые волны, ударные волны и уединенные волны — солитоны.

В линейной среде без дисперсии любая бегущая волна является стационарной, т.е. при распространении форма ее не меняется и она движется с постоянной скоростью. Причем все физические переменные в такой волне связаны алгебраически. Даже в слабо нелинейной среде при отсутствии дисперсии все гармоники, порождаемые нелинейностью, находятся в синхронизме с основной волной (все они распространяются с одинаковыми скоростями). Поэтому, спустя достаточно большое время, даже при очень слабой нелинейности, амплитуда их будет нарастать, что приведет к существенному изменению профиля волн, т.е. в нелинейных средах без дисперсии стационарных волн не бывает. На спектральном языке сказанное означает, что спектр исходного возмущения будет непрерывно расширяться в сторону больших частот. В результате в спектре волны появляются бесконечно высокие частоты, что и соответствует возникновению бесконечно быстрых перепадов на фронте волны.

Ударные волны.Обсудим теперь такое нелинейное волновое явление, как ударная волна. Об ударных волнах знают все, но подобно герою Мольера, не подозревают об этом. Проще всего ударную волну наглядно представить, как крутой и тонкий волновой фронт. «Тонкий» означает, что, например, на уровне моря его толщина в воздухе составляет порядка 0,025 мкм (для сравнения, длина световой волны в инфракрасной области составляет около 1 мкм). Когда в газообразном, жидком или твердом веществе внезапно высвобождается или вводится в него извне энергия, приводя к взрыву, возникает ударная волна. Рассмотрим в качестве примера динамику ударной волны при сферическом взрыве, когда химическая или ядерная энергия за милли- или микросекунды, т.е. по существу, внезапно, высвобождается в воздухе, в воде или под землей (см. рис. 6.8, на котором представлена фотография ядерного взрыва). При этом образуется сферический объем раскаленного газа, который находится под высоким давлением и, расширяясь, вызывает в окружающей среде ударную волну. Она движется наподобие приливной волны и практически мгновенно повышает давление, плотность и температуру среды. Кроме того, ударная волна создает поток вещества, следующий за ней. Охватывая все большие объемы вещества, сферическая ударная волна постепенно затухает, превращаясь в слабое возмущение или звуковую волну. Причем, вблизи от источника взрыва, когда давление, температура, плотность и скорость ударной волны велики, затухание происходит очень быстро. Затухание почти прекращается по мере превращения ударной волны в звуковой импульс. При распространении сильной ударной волны в невозмущенной среде давление, температура и плотность возмущенного состояния увеличиваются во много раз. Именно из-за этого гибнут попавшие в зону действия ударной волны люди и животные, под действием внезапного и сильного изменения давления рушатся различные сооружения. Большой ущерб всему живому и сооружениям может нанести ветер, возникающий благодаря скорости потока вещества.

Рис. 6.8. Первый подводный ядерный взрыв, произведенный в ходе испытаний ядерного оружия в акватории Новой Земли

Раскаты и грохот грома, особенно вблизи грозовых разрядов — одни из самых сильных звуков, известных в природе. Еще больше бед приносят землетрясения, во время которых из-за разрыва земной коры под действием сдвига внезапно высвобождается механическая энергия, что приводит к возникновению волн нескольких типов. Эти волны распространяются по поверхности земли и под землей.

Результатом подводного землетрясения являются цунами, вызывающие страшные разрушения. Цунами кажутся «безобидными» в открытом море, где их высота не превышает 30 см. Но расстояние между гребнями может достигать сотен километров, так что в цунами сосредоточена огромная масса воды, движущаяся иногда со скоростью 180 км/ч. Цунами замедляются на скалистой прибрежной отмели, их высота достигает несколько десятков метров.

Еще одно природное явление, порождающее ударные волны, — извержение вулканов. Канонический пример — извержение в 1883 году вулкана на необитаемом острове вулканического происхождения Кракатау, расположенном между Явой и Суматрой. Ударная волна трижды обогнула земной шар. Взрыв был слышен на расстоянии более чем 4 800 км от источника; в атмосферу было выброшено порядка 4,6 куб. км вулканического пепла и других продуктов извержения; энергия взрыва была эквивалентна энергии 250 тыс. бомб, сброшенных на Хиросиму.

Ударные волны возникают как на Земле, так и в воздухе, когда о землю ударяется метеорит. По одной из гипотез знаменитый Тунгусский метеорит, который в 1908 году взорвался над Сибирью, представлял собой ледяное ядро кометы. Оно распалось, не долетев до Земли. Но тем не менее ударная волна, возникшая, когда он входил в атмосферу Земли, привела к тому, что был повален и сгорел весь лес на площади около 2 000 км².

Еще один вид ударной волны — звуковой удар, который мы слышим после пролета сверхзвукового самолета. При обычном разговоре увеличение давления по сравнению с атмосферным незначительно и составляет ~0,1 Па. В то время как звуковые удары, вызываемые современными сверхзвуковыми самолетами, во много раз сильнее и составляют ~100 Па. Когда самолет летит с дозвуковой скоростью, волны давления расходятся во всех направлениях. Их не услышишь — они слишком слабы. Ситуация соответствует картине концентрических кругов, расходящихся от места падения камешка в неподвижную воду. При переходе к сверхзвуковым скоростям слабые возмущения давления складываются, что и приводит к образованию двух конических ударных волн. У носовой части самолета находится вершина головной ударной волны, а у хвостовой части — хвостовая. Обе волны падают на поверхность Земли и отражаются обратно в атмосферу. Пространство перед головной волной не возмущено, и, следовательно, беззвучно. Сверхзвуковой самолет может быть виден, но звук от него не слышен до тех пор, пока конические ударные волны не достигли Земли и не отразились от нее. Мы слышим звуковой удар, когда самолет может уже скрыться из вида.

Уединенные волны (солитоны).Наблюдал и первым описал солитон великий инженер викторианской эпохи Джон Скотт Рассел более ста пятидесяти лет тому назад. И хотя это описание уже стало столь же распространенным, как и описание солдат, шагающих по мосту, оно столь поэтично и ярко, что трудно удержаться от его изложения. Вот какую картину рисует Рассел:

«Я полагаю, что наилучшее представление об этом явлении даст описание обстоятельств моего первого знакомства с ним. Я наблюдал за движением баржи, которую быстро тянула по узкому каналу пара лошадей, когда баржа неожиданно остановилась. Но масса воды, которую баржа привела в движение, не остановилась, а собралась у носа судна в состоянии интенсивного дви

Предыдущая 1 2 345 6 7 8 Следующая