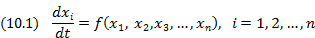ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Лекция десятая. Динамический хаос

Предыдущая 1 2 3 4 5 6 78Следующая

Как возникает случайность в динамической системе?Главная сила науки состоит в возможности предсказывать. Скажем, затмения можно предсказать на тысячу лет вперед на основе законов гравитации. Однако почему-то нельзя точно предсказать погоду, хотя атмосферные течения подчиняются физическим законам столь же строго. Нельзя точно предсказать течение горного ручья и рассчитать траекторию шара в биллиарде. В чем же дело? Почему в указанных явлениях теряется четкая связь между причиной и следствием? Пьер Симон Лаплас считал, что законы природы подразумевают полную предсказуемость и строгий детерминизм, а случайность — порождение несовершенства наблюдений. И более ста лет казалось, что в принципе он прав. Применение лапласовского детерминизма к социальным явлениям привело к известному философскому выводу об отсутствии свободной воли людей, о предопределенности их поведения.

Ощутимый удар лапласовскому детерминизму нанес Гейзенберг, который сформулировал принцип неопределенности в квантовой механике. Этот принцип утверждает, что нельзя одновременно точно измерить положение и скорость частицы. В частности, на основе этого принципа объясняется, почему процессы, происходящие в ядре (например, радиоактивный распад), принципиально нельзя предсказать, сколько бы информации о нем не собрали. Но, когда речь идет о непредсказуемости поведения крупномасштабных систем, принцип неопределенности ни при чем. Нужно искать другие объяснения.

Как может появиться случайность, а, следовательно, и непредсказуемость в детерминированной системе? Может ли динамическая система, описываемая уравнением вида

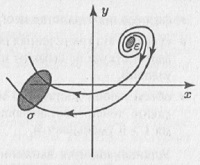
в которые не входят случайные функции, давать такое решение х_i = x_i(t), что при произвольном выборе х_i получаем случайную последовательность цифр? Не противоречит ли это известной теореме существования и единственности решения, которая гарантирует при заданных начальных условиях однозначное детерминированное поведение?

Если система обладает большим числом степеней свободы (например, газ в сосуде), то ситуация ясна: систему можно описать динамическим способом, но решение задачи становится нереальным. Дело в том, что мы не сумеем задать точно начальные координаты и скорости, допустим 10¹⁹ молекул, находящихся в 1 см³ газа. И если даже зададим, то ЭВМ не под силу рассчитать траектории такого числа частиц с учетом их столкновений друг с другом. Но как может появиться случайность в системе с небольшим числом степеней свободы, например, в идеализированном биллиарде, в котором шары катятся по столу и сталкиваются без потери энергии?

Дело в неустойчивости всех или почти всех траекторий системы. Игрок ударяет кием по шару, что приводит к серии столкновений. Предположим, что он полностью контролирует свой удар и хочет предсказать траекторию шара, по которому ударил. Так вот, если он пренебрежет даже гравитационным притяжением электрона на краю Галактики (очень слабое воздействие!), то его прогноз будет неправильным уже через минуту. Это объясняется тем, что шары не идеальны и малые отклонения от идеальной траектории, возникающие при каждом столкновении, нарастают, причем рост происходит экспоненциально. Таким образом, даже самое малое воздействие достигает макроскопических размеров. Это одно из основных свойств хаоса. Наиболее четко эту мысль выразили Н.С. Крылов, а затем Макс Борн. Определение детерминированности, данное М. Борном.

Каждое физическое состояние системы измеряется всегда с малой, но конечной неточностью ε. Поэтому оно определяется не числом, а некоторым вероятностным распределением. Задача состоит в том, чтобы на основе известного начального распределения предсказать распределения в момент времени t. Если данное решение устойчиво (начальное возмущение не нарастает), то любое последующее состояние предсказуемо, и система может считаться детерминированной. Такое определение детерминированности по М. Борну отличается от традиционного определения изменением последовательности предельных переходов при ε g 0 и t g ∞. Обычно сначала область начального рассеяния стягивается в точку, а затем смотрится поведение при t g ∞. Конечно, получается полная предсказуемость. Этот путь является нефизичным и заменяется другим: сначала при заданном ε определяется поведение траекторий и область конечного рассеяния при любом t, в том числе область рассеяния при t g ∞, а затем уже начальное рассеяние устремляется к точке. Если область конечного рассеяния при t g ∞ нарастает, то поведение системы непредсказуемо. Экспоненциальная неустойчивость траекторий, характерная для хаотической динамики, нанесла второй удар по детерминизму Лапласа. Существование хаоса гарантирует быстрое превышение пределов предсказуемости и опрокидывает «лапласовские надежды», что ошибки останутся ограниченными или будут хотя бы медленно расти, допуская в конечном счете долгосрочный прогноз.

Для возникновения хаоса в динамической системе необходимо, чтобы в фазовом пространстве системы:

• все (или почти все) соседние траектории внутри некоторой области разбегались; т.е., малый разброс начальных отклонений ε вел к тому, что при достаточно большом t уже нельзя было точно определить состояние системы, которая может находиться в любой точке области σ (рис. 10.1);

• все траектории оставались внутри ограниченного фазового объема.

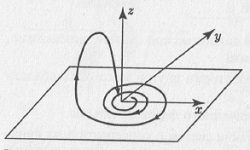
Рис. 10.1. Эволюция начального распределения на фазовой плоскости в случае неустойчивого состояния равновесия

Для консервативных динамических систем (т.е. систем без потерь), для которых их фазовый объем (с некоторой плотностью) по определению сохраняется справедлива теорема Пуанкаре о возвращении, которая гласит, что почти каждая точка любой области фазового пространства, двигаясь по траектории, вернется в эту область.

В трехмерном пространстве траектории могут разбегаться по двумерной поверхности, а возвращаться, выйдя в пространство. Траектория при этом может выглядеть, например, как раскручивающаяся плоская спираль, хвост которой, возвращаясь к ее началу, и вновь раскручивается (рис. 10.2 см. также рис. 5.8б). Располагаясь таким образом, траектория заполняет весь аттрактор, нигде не замыкаясь, и ведет себя сложно и запутанно.

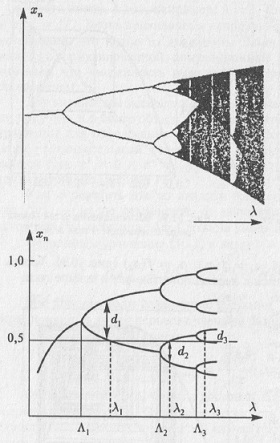
Рис. 10.2. Пример возвращающейся неустойчивой траектории, представляющей собой раскручивающуюся плоскую спираль, хвост которой, загибаясь к ее началу, и вновь раскручивается

Объект в фазовом пространстве, к которому стремятся все или почти все траектории и на котором они неустойчивы, называется странным аттрактором, в отличие от простых — состояний равновесия и предельных циклов. Странный аттрактор – объект, в котором траектории по одним направлениям разбегаются, по другим – притягиваются. Может быть, удивление подобным поведением и породило прилагательное «странный»? Ведь в простых аттракторах есть только притяжение. Как пишет Д.Рюэль в книге Случайность и хаос, странные аттракторы не являются гладкими кривыми или поверхностями, но имеют «не целую размерность», т.е., являются фрактальными объектами. Далее, и это еще более важно, движение на странном аттракторе выказывает чувствительную зависимость от начальных условий. И, наконец, при том, что странные аттракторы имеют лишь конечную размерность, временной анализ частот выявляет континуум частот... Возникла новая парадигма, которая получила имя — хаос, — данное ей Джимом Йорке, прикладным математиком, работающим в Университете Мэриленда. То, что мы сейчас называем хаосом, является временной эволюцией с чувствительной зависимостью от начальных условий.

Сценарии перехода к хаосу. В 1976 году американский специалист в области математической и теоретической физики Митчел Фейгенбаум сделал открытие, состоящее в том, что сценарий перехода к хаосу через бесконечный каскад бифуркаций удвоения периода универсален для большого класса динамических систем.

Что уже было известно к этому времени и могло стать источником вдохновения для Фейгенбаума? Во-первых, еще в 1971 году было обнаружено интересное свойство решений уравнений типа x_n₊₁ = λf(x_n): при изменении параметра λ существующее периодическое решение, имеющее период Т, теряет устойчивость, а устойчивым становится решение с периодом 2Т, затем 4Т и т.д. Интервал изменения параметра λ, в пределах которого цикл периода 2ⁿ устойчив, быстро сужается. Все значения λ, в которых происходит бифуркация удвоения периода, сгущаются к некоторому значению λ = λ_кр. Как только λ становится больше λ_кр внутри некоторой области фазового пространства, оказывается бесконечное число неустойчивых циклов. Вслед за этим сложным образованием сразу появляется хаотический (странный) аттрактор.

Во-вторых, к этому времени появились сомнения в сценарии возникновения турбулентности по Ландау. В работе Д. Рюэля (Франция) и Ф.Такенса (Нидерланды) возникновение турбулентности связывалось с появлением странного аттрактора, который возникал после небольшого числа (трех) бифуркаций. Разумеется, появилась идея связать непрерывный переход к турбулентности с возможностью реализации в течении бесконечного каскада бифуркаций удвоения периода. М. Фейгенбаум анализировал логистическое уравнение x_n₊₁ = λx_n(1 – x_n). Он хотел изучить комплексные аналитические свойства функций, порождаемых таким отображением. Уравнение аналитически не решалось, и Фейгенбаум занялся численными расчетами значений параметра λ, при которых происходило каждое удвоение. Фейгенбаум заметил, что значения параметров λ, соответствующие каждому удвоению, сходятся как геометрическая прогрессия. Это было удивительно: каждый последующий шаг можно было считать аналитически. Знаменатель прогрессии теперь носит название постоянной Фейгенбаума, его обозначают буквой δ, он равен 4,6692016...

В дальнейшем оказалось, что последовательность удвоений обладает свойством универсальности, которое не зависит от конкретных особенностей системы, а во многих случаях и от размерности фазового пространства. В чем же заключается эта универсальность? В том, что Фейгенбаум «выудил» геометрическую прогрессию: расстояние между значениями параметра λ_n, при котором рождается цикл периода 2ⁿ, и значением λ_кр, вслед за которым в системе возникает хаос, удовлетворяет условию (λ_кр – λ_n) = const δⁿ. Полученный Фейгенбаумом результат, в частности, означал, что если в эксперименте обнаружены несколько первых удвоений, то можно предсказать значение λ_кр, после достижения которого рождается хаос.

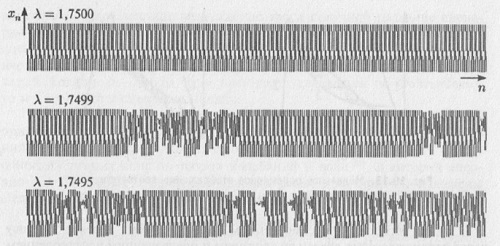
Рис. 10.3. «Поваленное фиговое дерево» (бифуркационная диаграмма) для логистического уравнения

Получается, что между хаосом и порядком существует глубокая внутренняя связь: непериодический случайный процесс получается, как предел рождения периодических структур, т.е. согласно сценарию Фейгенбаума, хаос есть цикл S^2∞. Независимо от конкретного вида системы, от степени ее сложности, теория Фейгенбаума дает вполне определенные количественные предсказания. Интересно, что по этому же сценарию (сценарию Фейгенбаума или, как его еще называют «переход к хаосу через каскад удвоений периода») возникает хаос и в нелинейных динамических системах, описываемых дифференциальными уравнениями, причем в таких системах опять появляются картины, аналогичные рис. 10.3, на котором показано «поваленное фиговое дерево».

Другие сценарии возникновения хаоса: перемежаемость и разрушение квазипериодических колебаний.Наиболее часто встречающийся в приложениях переход к хаосу — перемежаемость, который впервые описали французские физики П. Манневиль и И. Помо в 1980 году. На осциллограмме перемежаемость выглядит как постепенное (при изменении параметра) исчезновение периодических колебаний за счет их прерывания хаотическими всплесками (рис. 10.4).

Рис. 10.4. Зависимость переменной х от дискретного времени n для логистического отображения при переходе от цикла периода 3 к хаосу по сценарию перемежаемости с уменьшением управляющего параметра λ

Если в системе возник хаос, то возникает вопрос: «Насколько она хаотична?» Статистической характеристикой хаоса служит размерность странного аттрактора, которая отличается от привычной размерности линии, плоскости, объема. Оказывается, что странные аттракторы демонстрируют фрактальную структуру, и, соответственно, их размерность, является дробной.

На этом хочется поставить точку в обсуждении весьма непростых вопросов, касающихся сложного нерегулярного поведения детерминированных динамических систем (явления динамического или детерминированного хаоса). Для тех, кто захочет более глубоко и подробно познакомиться с этими вопросами, можно порекомендовать курс лекций профессора С.П. Кузнецова Динамический хаос.

Рекомендуемая литература

1. Андронов А. А., Витт А. А., Хайкин С. Э. Теория колебаний. М.: Наука, 1981.

2. Арнольд В. И. Теория катастроф. М.: URSS, 2009.

3. Берже П., Помо И., Видаль К. Порядок в хаосе. О детерминистическом подходе к турбулентности. М.: Мир, 1991.

4. Ван-Дейк М. Альбом течений жидкости и газа. М.: Мир, 1986.

5. Вартофский М. Модели. Репрезентация и научное понимание / Пер. с англ. М.: Прогресс, 1988.

6. Гласс И. Ударные волны и человек. М.: Мир, 1977.

7. Глейк Дж. Хаос. Создание новой науки. СПб.: Амфора, 2001.

8. Данилов Ю.А. Лекции по нелинейной динамике. М.: 3-е изд. М.: Книжный дом «Либрокомл/URSS, 2010.

9. Данилов Ю.А., Кадомцев Б.Б. Что такое Синергетика? // Нелинейные волны. Самоорганизация. М.: Наука, 1983; С. 5–16.

10. Данилов Ю.А. Роль и место синергетики в современной науке // Онтология и эпистемология синергетики. М.: ИФ РАН, 1997. С. 5–11.

11. Жилин Д.М. Теория систем. Опыт построения курса – М.: Либроком, 2004. – 176 с.

12. Зарубин В. С. Математическое моделирование в технике. М.: МГТУ им. Н.Э. Баумана, 2001.

13. Иванов Б.Н. Мир физической гидродинамики. М.: URSS, 2002.

14. Капица С. П., Курдюмов С. П., Малинецкий Г. Г. Синергетика и прогнозы будущего. М.: Наука, 1997; 3-е изд. М.: URSS, 2003.

15. Климонтович Ю.Л. Введение в физику открытых систем. М.: Янус-К, 2002.

16. Князева Е. Н., Курдюмов С. П. Основания синергетики. М.: Книжный дом Либроком/URSS, 2010.

17. Кондратьев Н.Д. Большие циклы конъюнктуры и теория предвидения. – М.: Экономика, 2002. – 768 с.

18. Короновский А. А., Трубецков Д. И. Нелинейная динамика в действии. Саратов: Изд-во ГосУНЦ «Колледж», 2002.

19. Крайтчфилд Д. П., Фармер Дж. Д., Паккард Н.Х., Шоу Р. С. Хаос // В мире науки. 1987. №2. С. 16-28.

20. Краснощеков П. С., Петров А. А. Принципы построения моделей. М.: Изд-во МГУ, 1983.

21. Кузнецов С. П. Динамический хаос. М.: Физматлит, 2001.

22. Кузнецов А. П., Кузнецове. П., Рыскин Н. М. Нелинейные колебания. М.: Физматлит, 2002.

23. Малинецкий Г.Г, Потапов А. Б. Современные проблемы нелинейной динамики. М.: URSS, 2002.

24. Мандельброт Бенуа. Фрактальная геометрия природы. – Ижевск: Институт компьютерных исследований, 2010. – 676 с.

25. Математическое моделирование / Под ред. Дж. Эндрюса и Р. Мак-Лоуна; Пер. с англ. М.: Мир, 1979.

26. Моисеев Н.Н. Математика ставит эксперимент. М.: Наука, 1979.

27. Моисеев Н.Н. Расставание с простотой. – М.: Аграф, 1998. – 480 с.

28. Мун Ф. Хаотические колебания. М.: Мир, 1990.

29. Мышкис А. Д. Элементы теории математических моделей. М.: Книжный дом Либроком/URSS, 2009.

30. Неймарк Ю. И. Математические модели естествознания и техники. Н. Новгород, Вып. 1. 1994; Вып. 2. 1996; Вып. 3. 1997.

31. Николис Г., Пригожим И. Познание сложного. М.: Издательство ЛКИ/URSS, 2008.

32. Ньюэлл А. Солитоны в математике и физике. – М.: Мир, 1989. – 326 с.

33. Общероссийский естественно-научный журнал «Изв. высш. учеб. заведений. Прикладная нелинейная динамика».

34. Пайтген Х.-О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. М.: Мир, 1993.

35. Петерс Э. Хаос и порядок на рынках капитала. – М.: Мир, 2000. – 336 с.

36. Постон Т., Стюарт И. Теория катастроф. М.: Мир, 1980.

37. Рыскин Н. М., Трубецков Д. И. Нелинейные волны. М.: Физматлит, 2001.

38. Рюэль Д. Случайность и хаос. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 192 с.

39. Синергетическая парадигма: Многообразие поисков и подходов. М.: Прогресс-Традиция, 2000.

40. Синергетическая парадигма: Нелинейное мышление в науке и искусстве. М.: Прогресс-Традиция, 2002.

41. Синергетическая парадигма: Человек и общество в условиях нестабильности. М.: Прогресс-Традиция, 2003.

42. Сноу Ч. П. Две культуры. М.: Прогресс, 1973.

43. Соросовский образовательный журнал

44. Стасенко А.Л. Волны на воде и «Заморские гости» Рериха // Квант. 1972. № 9. С. 10. (Статья повторно напечатана в журнале: Квант. 1990. № 1. С. 24-29, 62).

45. Тарасенко В. Фрактальная логика. М.: Книжный дом Либроком/URSS, 2009.

46. Тоффлер Э. Третья волна. – М.: АСТ, 2002. – 784 с.

47. Тоффоли Т., Марголус Н. Машины клеточных автоматов. М.: Мир, 1991.

48. Трубецков Д.И., Мчедлова Е. С., Красичков Л. В. Введение в теорию самоорганизации открытых систем. М.: Физматлит, 2002.

49. Трубецков Д. И., Рожнев А. Г. Линейные колебания и волны. М.: Физматлит, 2001.

50. Трубецков Д.И. Введение в синергетику. Колебания и волны. М.: URSS, 2003.

51. Трубецков Д.И. Введение в синергетику. Хаос и структуры. М.: URSS, 2004.

52. Трубецков Д.И. Колебания и волны для гуманитариев. Саратов: Изд-во ГосУНЦ «Колледж», 1997.

53. Федер Е. Фракталы. М.: Мир, 1991.

54. Фейнберг Е. Л. Две культуры. Интуиция и логика в искусстве и науке. Фрязино: «Век2», 2004.

55. Филиппов А.Т. Многоликий солитон. М.: Наука, 1990.

56. Хакен Г. Синергетика. Иерархия неустойчивостей в самоорганизующихся системах и устройствах. М.: Мир, 1985.

57. Хакен Г. Тайны природы. Синергетика: наука о взаимодействии. – Ижевск: Институт компьютерных исследований, 2003. – 320 с.

58. Хорафас Д.Н. Системы и моделирование. М.: Мир, 1967.

59. Шустер Г. Детерминированный хаос. М.: Мир, 1988.

60. Эткинс П. Порядок и беспорядок в природе. М.: Мир, 1987.

Предыдущая 1 2 3 4 5 6 78Следующая