ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Лекция девятая. Клеточные автоматы

Предыдущая 1 2 3 4 5 678 Следующая

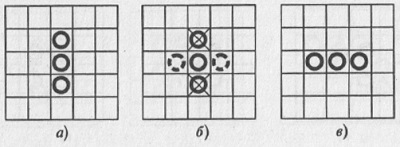
Клеточные автоматы были задуманы в конце сороковых годов нашего столетия Дж. фон Нейманом и К. Цусе как универсальная вычислительная среда для построения алгоритмов. Клеточный автомат представляет собой некоторое дискретное пространство, на котором происходит эволюция, и набор правил, по которым эта эволюция осуществляется. Самым знаменитым клеточным автоматом является так называемая игра Жизнь, предложенная в 1970 году математиком Джоном Конуэем. Можно считать, что игра «Жизнь» описывает популяцию неких вымышленных организмов, развивающуюся во времени и пространстве в соответствии с заданными законами размножения и вымирания. Исследуя эволюцию этих организмов, можно отчетливо наблюдать процессы самоорганизации и структурообразования.

Пространством, на котором происходит эволюция, в игре «Жизнь» является плоскость, разделенная на квадратные ячейки. Размеры доски (количество ячеек по вертикали и горизонтали) могут быть различными — читатель может экспериментировать на обычной шахматной доске размером 8x8 клеток, хотя предпочтительнее, разумеется, отслеживать эволюцию с помощью компьютера. В дальнейшем будем рассматривать бесконечные доски, т. е. доски с таким большим числом клеток, что границы доски не достигаются, а, следовательно, не играют существенной роли.

Будем называть клетку «живой», если на ней находится фишка, в противном случае будем считать ее «мертвой» или «пустой». Время в игре «Жизнь» дискретно и измеряется в поколениях: каждый момент дискретного времени соответствует одному поколению. Существует набор простых правил, описывающих рождение и гибель клеток от поколения к поколению:

1. Каждая живая клетка, у которой имеется две или три живые соседние клетки, выживает и переходит в следующее поколение.

2. Каждая живая клетка, у которой оказывается меньше двух живых соседей, в следующем поколении погибает от одиночества.

3. Каждая живая клетка, у которой оказывается больше трех живых соседей, в следующем поколении погибает от перенаселенности.

4. В каждой пустой клетке, у которой оказывается ровно три живых соседа, в следующем поколении рождается новая жизнь.

Набор эволюционных правил очень прост, а эволюция живых клеток из поколения в поколение может быть очень сложной и красивой. Именно поэтому игра «Жизнь» завоевала широкую известность и стала классическим объектом той части синергетики, которая связана с самоорганизацией и структурообразованием. Рассмотрим эволюцию триплета (в игре «Жизнь» триплетом называется любая конфигурация из трех живых клеток), изображенного на рис. 9.1а. Как нетрудно видеть, из набора эволюционных правил игры «Жизнь» следует, что верхняя и нижняя клетки конфигурации погибают от одиночества (на рис. 9.1б они зачеркнуты). Центральная же клетка имеет двух живых соседей, поэтому она выживает и переходит в следующее поколение. Кроме этого, на двух клетках, прилегающих к триплету, рождается в следующем поколении новая жизнь (см. рис. 9.1б). Особо следует отметить, что гибнущие клетки погибнут только в следующем поколении, а, следовательно, в настоящий момент времени (несмотря на то, что они в следующий момент времени погибнут) эти клетки продолжают оказывать влияние на эволюцию системы. Точно также рождающиеся клетки появятся на игровом поле лишь в следующем поколении, и значит, в текущем поколении они никакого влияния на эволюцию системы не оказывают.

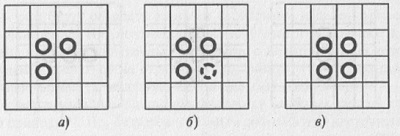
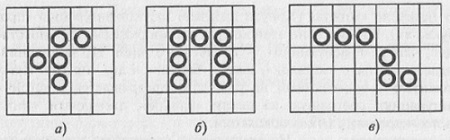
Рис. 9.1. Эволюция триплета «мигалка»: а) начальная конфигурация в первом поколении; б) то же самое первое поколение, с указанием гибнущих и рождающихся клеток; в) конфигурация «мигалка» во втором поколении

Таким образом, в следующем, втором поколении начальная конфигурация из трех вертикальных клеток превращается в три живые клетки, расположенные горизонтально (рис.9.1в). Нетрудно понять, что в следующем (третьем) поколении конфигурация будет полностью повторять первоначальную. Иными словами, исходная конфигурация оказывается периодической с периодом 2 (воспроизводит себя на втором ходу) — она попеременно превращается то в вертикальный, то в горизонтальный ряд из трех живых клеток. За свое поведение этот триплет был назван «мигалкой» или «семафором».

Другой триплет, показанный на рис. 9.2а, в следующем поколении превращается в устойчивую конфигурацию под названием «блок» — нетрудно видеть, что любая клетка из этой конфигурации имеет трех живых соседей, а следовательно, переходит в следующее поколение. Подобные стационарные структуры довольно часто появляются в ходе эволюции. Конуэл называет их «любителями спокойной жизни».

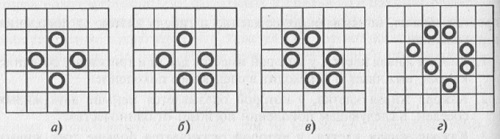
Рис. 9.2. Исходный триплет (а); тот же самый триплет с указанием рождающейся клетки (б) и второе поколение — устойчивая конфигурация «блок» (в)

Нетрудно видеть, что остальные триплеты, отличные от только что описанных (разумеется, не считая тех триплетов, которые совпадают с вышеописанными при повороте или зеркальном отражении) быстро погибают в ходе эволюции. На рис. 9.3 приведены еще несколько часто встречающихся стационарных конфигураций, а на рис. 9.4 — две периодические конфигурации. Первая из них (рис. 9.4а) называется «опрокидывателем», поскольку каждые семь поколений верх и низ у этой конфигурации меняются местами, а конфигурация, приведенная на рис. 9.4б, имеет период, равный четырем.

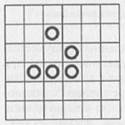
Рис. 9.3. Некоторые стационарные структуры, возникающие в игре «Жизнь»: а) бадья; б) лодка; в) корабль; г) каравай

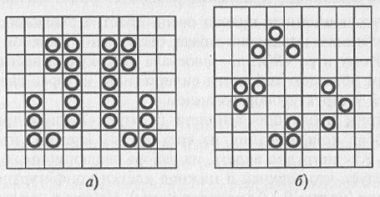
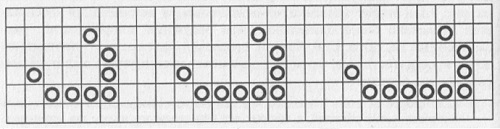
Рис. 9.4. Периодические конфигурации игры «Жизнь»

Таким образом, уже из рассмотрения простейших конфигураций можно сделать вывод о том, что в игре «Жизнь» возможны следующие виды эволюционного развития популяции:

1. Популяция полностью вымирает через конечное число поколений.

2. Популяция с течением времени превращается в стационарную структуру, которая больше не изменяется.

3. Из первоначальной популяции возникает периодически изменяющаяся во времени структура.

Следует отметить, в игре «Жизнь» существуют конфигурации, называемые «долгожителями» — это конфигурации, состоящие менее чем из десяти живых клеток, у которых устойчивое состояние не достигается в течение по крайней мере пятидесяти поколений. Несколько таких долгожителей представлены на рис. 9.5. Конфигурация, представленная на рис. 9.5а, носит название «r-пентамино», а ее эволюция оказывается несколько более длительной, чем эволюции конфигураций, рассмотренных до этого. Сам Конуэй проследил эволюцию «r -пентамино» до четыреста шестидесятого хода и описывает достигнутую конфигурацию следующим образом: «...от фигуры осталось множество мертвых (не изменяющихся) обломков и лишь несколько малых областей, в которых все еще теплилась жизнь, так что отнюдь не очевидно, что процесс эволюции должен происходить бесконечно долго».

Рис. 9.5. Конфигурации в игре «Жизнь», названные «долгожителями»

Однако эта конфигурация эволюционирует еще некоторое время и превращается в периодически пульсирующую конфигурацию с периодом 2 лишь после 1 103 поколений. Конфигурация, изображенная на рис. 9.5б, носит название «ворота» (Конуэй называет эту конфигурацию «прописная буква π»). Время жизни этой конфигурации оказывается существенно меньше, чем у «r-пентамино» — после всего лишь 173 поколений она распадается на пять «мигалок», шесть «блоков» и два «пруда». Наконец, «долгожитель», приведенный на рис. 9.5в, превращается в устойчивую конфигурацию, состоящую из шести «блоков», двенадцати «мигалок» и одного «каравая» в 609-м поколении.

Но оказывается, возможные сценарии эволюции не ограничиваются приведенными выше. Существует еще один класс структур в игре «Жизнь», которые эволюционируют периодически не только во времени, но и в пространстве. На рис. 9.6 приведена простейшая пространственно-временная периодическая структура, называемая «глайдером» (от англ. to glide — скользить). Подобные перемещающиеся конфигурации называются «космическими кораблями» (рис. 9.7). «Глайдер» считается «космическим кораблем» легчайшего веса, так как все остальные космические корабли состоят из большего числа живых клеток. Во время полета «космических кораблей» (исключая «глайдер») из них вылетают «искры», которые тут же гаснут при дальнейшем движении «кораблей». «Космические корабли» не могут занимать в длину более шести клеток, в противном случае на доске начинают появляться различные мелкие конфигурации, препятствующие дальнейшему движению «космического корабля», что ведет, в конце концов, к его разрушению и гибели. Однако, как выяснил Конуэй, таким «космическим кораблям» (их называют «сверхтяжелыми») необходим эскорт из двух или большего числа «кораблей» меньших размеров. Эскорт не дает возникать различным препятствиям на пути «сверхтяжелого космического корабля».

Рис. 9.6. Глайдер (пространственно-временная периодическая структура, которая воспроизводит себя через четыре хода, сдвигаясь на одну клетку вниз и вправо)

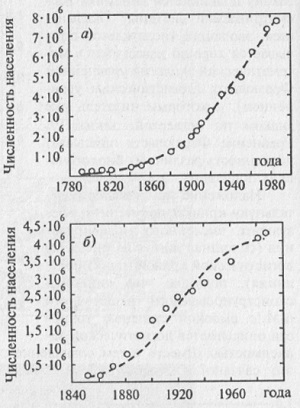
Рис. 9.7. Космические корабли

Таким образом, к возможным видам эволюционного развития, описанным выше, следует добавить:

4. Популяция развивается в течение длительного интервала дискретного времени, не погибая и не повторяя себя в своем развитии.

5. Популяция является периодической пространственно-временной структурой, периодически изменяющейся во времени и передвигающейся по эволюционному пространству.

6. Популяция является неограниченно растущей, на бесконечном эволюционном пространстве ее численность растет неограниченно.

Любая конфигурация порождает в игре «Жизнь» только одну конфигурацию-наследника, а вот конфигураций-родителей может быть несколько. Иными словами, зная текущую конфигурацию живых клеток, можно однозначно определить конфигурацию, которая появится в следующем поколении, но вот однозначно определить конфигурацию, существовавшую на эволюционном пространстве в предшествующий момент дискретного времени, невозможно, поскольку текущая конфигурация в общем случае может быть порождена несколькими различными конфигурациями. С другой стороны, существуют такие конфигурации, у которых нет «конфигураций-родителей». Такие конфигурации называются «садами Эдема». Понятно, что «сад Эдема» не может появиться в результате эволюционного развития, а должен быть искусственно привнесен извне. Другим интересным моментом является то обстоятельство, что хотя эволюционные правила известны и их число невелико, предсказать заранее (как говорят, a priori) результат эволюции невозможно, пока последовательно не будут пройдены все поколения от начальной конфигурации до искомой.

Если вообразить достаточно большое количество «первичного бульона» из хаотически распределенных живых клеток, то можно ли ожидать появление в эволюционном пространстве каких-либо самовоспроизводящихся существ, а также того, что наиболее приспособленные из них к выживанию будут благополучно здравствовать дольше других. Поиграть в «Жизнь» можно здесь.

Искусственная жизнь.Перейдем теперь от клеточных автоматов к рассмотрению направления, связанного с исследованием эволюционных процессов, называемого Artificial Life (AL) — искусственная жизнь. В основе этого направления лежит чрезвычайно смелая (наверное, можно даже сказать, дерзкая) идея перенести эволюционные процессы в другую, неуглеродную среду. Подобной средой может стать оперативная память компьютера. Речь не идет о моделировании каких-либо процессов биологических объектов, реально существующих в нашем мире, с помощью электронных вычислительных машин. Компьютер выступает в этом случае не как средство моделирования, а скорее, как среда обитания, в которой могут существовать «цифровые организмы», живущие и эволюционирующие по другим законам цифрового мира.

Еще один вопрос, связанный с цифровой эволюцией, — вопрос о возможности возникновения «цифрового интеллекта». Эта тема является благодатной почвой для научно-фантастических произведений. В настоящее время трудно сказать по этому поводу что-либо определенное, но если возникновение «цифрового разума» и возможно, то, по всей вероятности, он может существенно отличаться от разума «биологического», поскольку ход эволюционного развития цифровой жизни происходит по другим законам, нежели развитие биологической жизни. С другой стороны, возможно существование общих закономерностей эволюционного развития, свойственных самым различным формам жизни, а, следовательно, и «цифровой разум» (конечно, если его возникновение возможно) может быть похож на разум биологический. Но пока все это остается лишь на уровне гипотез, и дать ответы на поставленные вопросы может лишь время (отдаленное от нас, а может быть и не очень).

Что могут дать человечеству исследования в области искусственной жизни. С одной стороны, эти исследования могут служить ключом к пониманию наиболее общих закономерностей эволюционного развития. С другой стороны, если люди научатся понимать эти закономерности, то, вмешиваясь в естественный ход эволюции цифровой жизни, внося изменения в структуру организмов, проводя селекцию организмов с нужными свойствами, может быть, удастся «вырастить» программные продукты (например, операционные системы, которые управляют работой компьютеров) с такими возможностями, которые сегодня даже трудно себе и представить. Понимание же наиболее общих закономерностей эволюционного развития может быть использовано и при селекции новых биологических видов.

Клеточные автоматы и моделирование динамики биологических популяций.У читателя вполне может сформироваться впечатление, что клеточные автоматы — это не более чем забавная игрушка. Однако это совершенно неверное представление. Научные исследования с использованием клеточных автоматов на сегодняшний день привлекают к себе все большее внимание ученых в самых различных областях науки. Во многом этому способствует бурное развитие вычислительной техники, без которой изучение моделей типа клеточных автоматов было бы практически невозможно.

Особенно интересен вопрос о возможности моделирования динамики различных биологических популяций с помощью клеточных автоматов. Рассмотрим клеточный автомат, с помощью которого удалось объяснить некоторые закономерности динамики численности народонаселения земного шара в тех или иных локальных областях. Такой клеточный автомат, подчиняющийся своим правилам (похожим, но не идентичным правилам в игре «Жизнь»), называют решеточным газом.

«Решеточный газ есть набор „атомов", положение в пространстве каждого из которых может принимать только дискретные значения. Это дискретное положение атома на каждом последующем дискретном шаге во времени определяется геометрией решетки, которая в свою очередь определяется ближайшими γ соседями каждой клетки решетки. В каждой клетке может находиться не более одного атома...»

Оказывается, эволюция числа клеток описывается хорошо известным в математической экологии уравнением Ферхюльста (логистическим уравнением). Интерес к модели решеточного газа и результатам, полученным с помощью нее, объясняется возможностью качественного описания особенностей пространственно-временной динамики численности «реальных» популяций. Обсудим в этом контексте некоторые проблемы демографии и, в частности, динамику численности народонаселения тех или иных локальных областей, используя результаты, полученные с помощью решеточного газа. В качестве примера приведем некоторые демографические данные численности населения США за последние 200 лет, которые были получены из базы данных университета Вирджинии.

Если рассмотреть динамику численности населения различных американских штатов, то можно заметить, что наблюдается разделение штатов на две большие основные группы (см. Короновский А. А., Лопатников Д. И., Храмов А. Е. Некоторые аспекты изменения численности народонаселения США с точки зрения нелинейной динамики). У первой группы, в которую были включены штаты, входившие в состав США с самого момента образования (данные территории начали заселяться с самого начала колонизации американского континента), — Флорида, Алабама, Южная и Северная Каролина, Нью-Йорк, Коннектикут и др., численность населения как функция времени хорошо описывается логистической кривой (см. рис. 9.8а, на котором представлена зависимость численности населения штата Нью-Йорк). Заметим также, что у этих штатов наибольшая плотность населения, и, как следствие, наиболее однородное распределение населения по территории.

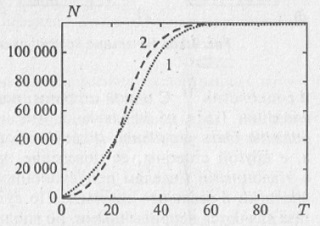
Рис. 9.8. Динамика численности народонаселения штатов: а) Нью-Йорк и б) Миннесота. Пунктиром показаны соответствующие логистические кривые, наилучшим образом аппроксимирующие демографические данные. Здесь кружки — демографические данные начиная с 1780 года и интервалом в 10 лет

Другую группу составляют штаты, присоединенные к США существенно позже. Это внутренние территории, которые вначале были свободными (на них проживали индейские племена), затем начиналась их колонизация, на них появлялись переселенцы, земли получали статус территорий, на которые правительство США заявляло свои претензии, и затем соответствующие территории получали статус штатов. Это штаты Айова, Миннесота, Колорадо, Канзас, Оклахома и т.д. Для этих штатов типична динамика численности населения, приведенная на рис. 9.8б (он соответствует штату Миннесота, который до 1849 года был так называемой неорганизованной территорией, затем получил статус территории и только в 1858 году стал полноправным штатом). Для этих штатов, для которых характерно постепенное заселение (с одной стороны, здесь играли роль большое число переселенцев, с другой стороны — имело место коренное население), численность населения сначала обгоняла соответствующую логистическую кривую, а затем отставала от нее.

Интересно, что динамика решеточного газа, описывающего распространение «клеточной» популяции на территорию, на которой уже есть население, демонстрирует аналогичную динамику численности популяции. На рис. 9.9 приведена зависимость числа активных клеток решеточного газа N от дискретного времени. Начальные условия выбраны так, что имеется небольшая область с высокой плотностью активных клеток, а остальная область моделирования заполнена равномерно небольшим числом клеток. Сравнивая рис. 9.8б и 9.9, видно, что динамика обеих систем качественно подобна. Итак, следует признать, что «клеточная» (или «решеточная») популяция может оказаться весьма эффективным инструментом для исследования различных задач в биологии, экологии и даже демографии и социологии.

Рис. 9.9. Динамика численности «клеточной» популяции, распространяющейся на территорию, где уже есть население с небольшой плотностью расселения. Кривая 1 соответствует решеточному газу, 2 — уравнению Ферхюльста (сравни с рис. 9.8б)

Предыдущая 1 2 3 4 5 678 Следующая