ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Лекция третья. Математические понятия, без которых не обойтись
Почему в нашем курсе много физики и математики?Синергетика во многом «берет» свое начало из естественных наук. Кроме того, математический аппарат, который с успехом в них применяется, обеспечивает универсальность описания явлений различной природы. Система — множество элементов, находящихся в отношениях и связях друг с другом, образующих определенную целостность, единство. В недавно вышедшей книге Д.М. Жилина Теория систем приведено такое определение: свойство совокупности, которое не является суммой или средневзвешенным свойством отдельных компонентов совокупности, называется эмерджентным свойством. Совокупность, обладающая эмерджентным свойством, называется системой. Величины, которые можно измерить (сравнить с однородной величиной, принятой за единицу измерения), называют физическими. Отметим, что отнюдь не все величины можно измерить. Например, «красота» не имеет эталонов, с которыми можно было бы провести количественное сопоставление — измерить. Размеры (численные значения) величин, типичные для данной системы, будем называть характерными масштабами данной системы (рис. 3.1, 3.2).
Рис. 3.1. Характерные пространственные масштабы
Рис. 3.2 Характерные временные масштабы Время, в течение которого протекают процессы, в физических системах существенно меньше, чем в системах социальных. Некоторые процессы в социальных системах могут иметь характерный временной масштаб, сопоставимый (или даже превышающий) время человеческой жизни. Поэтому для исследования подобных процессов в социальных системах может потребоваться время, равное времени жизни нескольких поколений. На таких временных масштабах очень сильно меняются методика сбора данных, подходы к их обработке и т.п. Все это очень затрудняет исследование социальных систем. Физические системы с этой точки зрения существенно более удобны — характерное время процессов, протекающих в таких системах, существенно меньше времени человеческой жизни, что позволяет исследователям проводить серии экспериментов за небольшой промежуток времени. Воспроизвести по-новому еще раз ситуацию в социальной системе невозможно: если исследователя интересует какое-либо историческое событие (скажем, революция), то нельзя «вернуть» ситуацию «на исходные позиции» и после этого снова «запустить» процесс. Историк вынужден иметь дело с историческими документами, которые несут на себе отпечаток субъективных оценок; исторические документы могут быть искажены или даже фальсифицированы. Наконец, в физической системе можно спланировать и провести интересующий эксперимент, в то время как поставить эксперимент в социальной системе существенно более проблематично. Именно поэтому физические системы оказались более хорошо изученными как экспериментально с помощью хорошо развитого в физике инструментария и методик, так и теоретически с использованием математического аппарата; по ним накоплен большой объем данных. Численные значения характеризующих систему величин. Переменные и параметры.Для того чтобы охарактеризовать систему, используется определенный набор величин. Все величины можно разделить на параметры и переменные. Переменные — это величины, которые могут изменяться при рассмотрении процесса, а параметры — это такие величины, которые в рамках рассматриваемой задачи могут считаться постоянными (такое деление в некоторой степени условно). Переменные величины, в свою очередь, подразделяются на независимые переменные и зависимые (которые также называют функциями). Под независимыми переменными понимают такие переменные величины, которые в рамках данной задачи изменяются независимо от рассматриваемой системы. В качестве независимых переменных, как правило, выделяют время и пространственные координаты. Математиками найдено огромное число различных функций. К наиболее популярным относятся линейная, квадратичная зависимости, гармонические функции у = sin(х), у = cos(x) и экспонента у = ех. Динамический и статистический подходы к описанию объектов и явлений.Динамический подход к описанию объектов и явлений является отражением детерминизма (учение о закономерности и причинной обусловленности всех явлений природы и общества). В рамках этого подхода предполагается, что если точно задать все начальные условия и указать все факторы, которые влияют на поведение рассматриваемой системы, то можно сколь угодно точно и однозначно предсказать все последующие состояния системы). Статистический (вероятностный) подход не претендует на точное описание и прогноз состояния системы. Центральным моментом здесь является понятие «вероятность», и описание системы сводится к заключению о том, что некоторое событие может произойти (а может и не произойти) с некоторой вероятностью. Линейность и нелинейность.Функция является линейной, если ее графиком является прямая линия, а в формуле, задающей вид функции, отсутствуют нелинейные слагаемые (рис. 3.3).
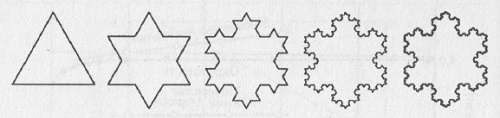
Рис. 3.3. Примеры некоторых линейных и нелинейных функций На одинаковые приращения независимой переменной линейная функция беспристрастно (т. е. независимо от значения независимой переменной) откликается одинаковыми приращениями. Это означает, что линейная зависимость не обладает избирательностью. Она не может описывать ни резонансных всплесков, ни насыщения, ни колебаний — ничего, кроме равномерного неуклонного роста или столь же равномерного и столь же неуклонного убывания. Фракталы.Наряду с привычными геометрическими объектами – «прямая», «линия», «плоскость», «поверхность» – существует понятие «фрактал», с которым связано понятие фрактальной размерности. Под фракталами понимают множества, демонстрирующие на разных масштабах разрешения своей геометрической структуры свойства подобия в строгом или приближенном смысле, а также объекты в природе, обладающие этим свойством, хотя бы приближенно, в достаточно широком интервале масштабов. Понятие «фрактал» широко вошло в обиход благодаря математику Бенуа Мандельброту (подробнее см. Бенуа Мандельброт. (Не)послушные рынки: фрактальная революция в финансах). Ему принадлежит следующее определение: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому». Пример фрактала — снежинка Коха (рис. 5). Ее построение начинается с равностороннего треугольника, затем на каждой стороне средняя треть заменяется ломаной линией, состоящей из двух отрезков такой же длины. Эта процедура повторяется до бесконечности, в результате чего получается область с фрактальной границей.
Рис. 3.4. Построение снежинки Коха Еще один фрактальный объект — салфетка Серпинского. В его основе лежит равносторонний треугольник, который можно разбить на четыре одинаковых равносторонних треугольника и удалить центральный (рис. 3.5). То же самое проделывается с каждым оставшимся треугольником до бесконечности.
Рис. 3.5. Построение салфетки Серпинского Фрактальные объекты часто встречаются и в природе (рис. 3.6).
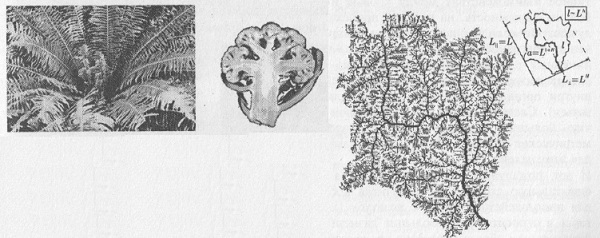
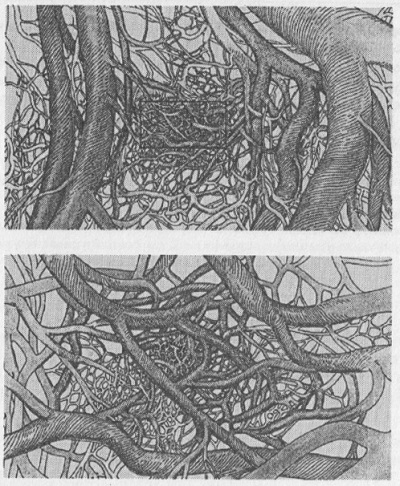
Рис. 3.6. Лист папоротника, цветная капуста, структура ручья Почему фрактальные объекты столь широко распространены в природе? Одной из причин является характерная особенность строения фракталов: фрактальный объект на плоскости занимает ограниченную площадь, в то время как его длина стремится к бесконечности. Аналогично, «объемные» фракталы характеризуются относительно малым объемом, но большой площадью поверхности. А это очень удобно для Природы! Действительно, какую функцию, например, выполняют легкие человека? Они должны обеспечивать эффективное взаимодействие между кровью и воздухом. Очевидно, что чем больше поверхность, на которой происходит такое взаимодействие, тем лучше. Аналогично, фрактальным образом устроена кровеносная система живых организмов (рис. 3.7), корневая система растений (здесь задача все та же — при малом объеме обеспечить большую поверхность соприкосновения) и пр.
Рис. 3.7. Фрактальная жизнь: строение кровеносной системы; нижний рисунок является увеличенным фрагментом верхнего |